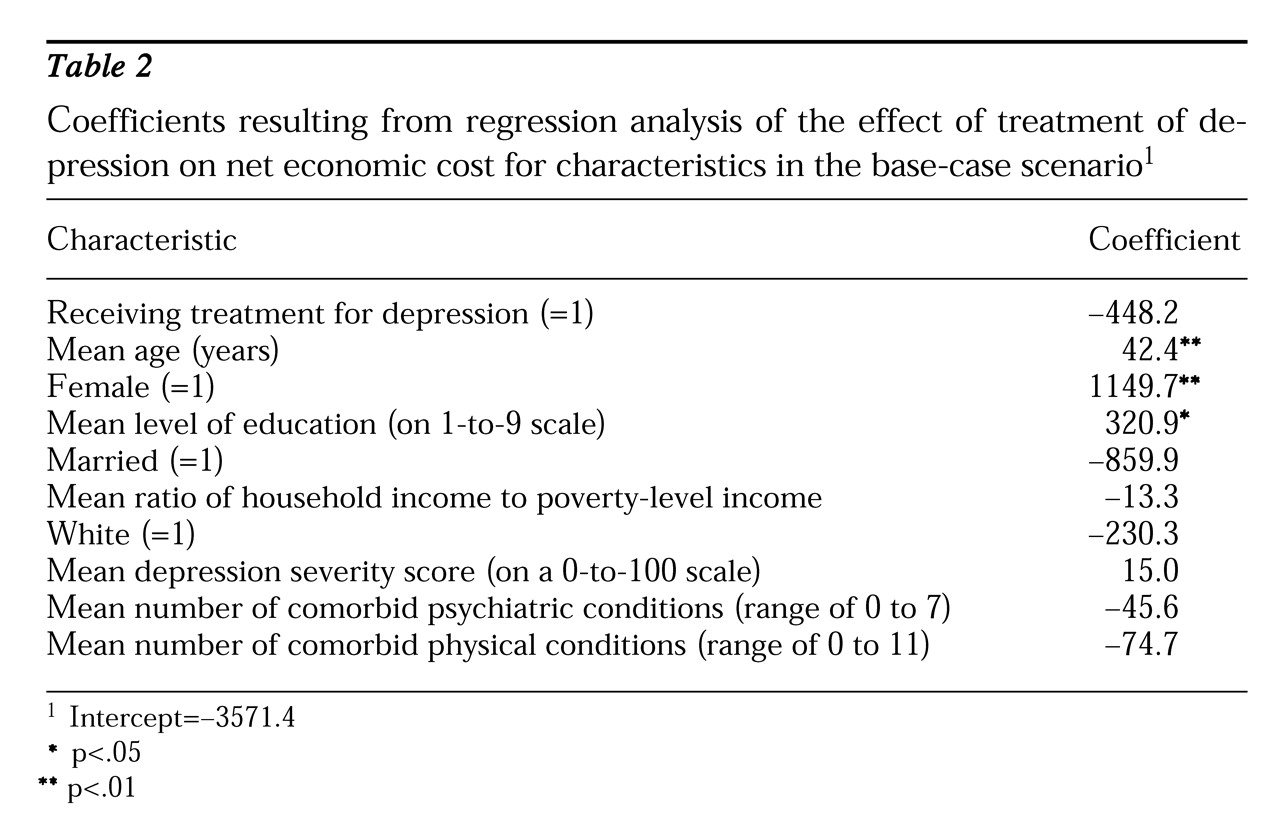
Sensitivity analyses
We performed sensitivity analyses in several alternative scenarios to examine the robustness of the result in the base-case scenario. In the base-case scenario, we did not take into account the potential selection bias. We performed a sensitivity analysis using instrumental variables to correct for selection bias (scenario A). In applying this method, we first estimated the probability of seeking treatment for depression using a nested logit model (
17). In this model, we used actual travel distances to mental health providers and primary care providers as predictors for choice of treatment for depression. Theoretically, travel time represents an appropriate instrumental variable because it affects the decision to seek treatment but does not affect outcomes directly. A geographic information system was used to code the geographic location of study subjects as well as all general medical providers (N=3,419) and mental health specialists (N=1,034) practicing in Arkansas and to calculate the travel times from each study subject to each provider. A three-level nested logit model was specified to estimate the sequential impact of travel times on choice of provider, choice of provider sector, and the decision to seek treatment.
Travel time was found to be a significant predictor of choice of provider in both the general medical and the specialty sectors (p<.001). The expected maximum utility of provider choice—a function of travel times to providers in each sector—was found to be a significant predictor of sector choice (p<.05) and, in turn, of the decision to seek depression treatment.
The predicated probability of seeking depression treatment from this nested logit model was then used in the regression analysis to estimate net economic cost, replacing the dummy variable indicating depression treatment in the base-case scenario. In this sensitivity analysis, the results indicated that the effect of depression treatment on net economic cost was -$1,118 (p=.7). Thus the estimated effect was magnified, from -$448 to -$1,118. However, the standard error of the estimate increased as well, due to the application of instrumental variables, resulting in a nonsignificant parameter estimate. Thus we can conclude again that depression treatment had no statistically significant effect on net economic cost and that depression treatment paid for itself.
In the base-case scenario, if the visit was also for physical or other problems, we allocated 50 percent of the charges as costs of treatment for depression. This allocation was arbitrary. We therefore performed a sensitivity analysis by allocating 100 percent of the charges as costs of treatment for depression for those visits (scenario B). The same regression analysis used in the base-case scenario was used in scenario B. The estimated treatment effect on net economic costs was -$420 (p=.4). We also performed a regression analysis using 0 percent as the allocation of depression treatment costs (scenario C). In this scenario, the estimated effect of depression treatment on net economic costs was -$476 (p=.3). In both of these scenarios, the results were essentially the same as that of the base-case scenario.
From the societal perspective as well as the patient's perspective, the time consumed in receiving treatment—including travel time, waiting time, and time seeing the provider—should be considered part of the cost of treatment. We performed an analysis including an estimated time cost as part of the treatment cost (scenario D).
Specifically, for outpatient visits that were exclusively for depression we assumed the total time consumed was three hours for each visit. For outpatient visits that were partly for depression, we assumed that one and a half hours was spent for treatment of depression. For inpatient admissions, we assumed eight hours a day for each hospital stay. Then the total number of hours was prorated by the ratio of depression charges to the total charge for the stay. The cost of patient time was estimated by the number of hours multiplied by a subject's wage rate. The estimated effect of depression treatment on net economic cost in this scenario was -$399 (p=.4). Again, the cost of depression treatment was offset by the savings in reduced lost earnings, or depression treatment paid for itself.
Recent research on cost of illness suggests that the human capital approach used to calculate indirect costs or lost earnings in our study may overestimate actual costs (
18,
19). In some occupations, for example, the economic cost of absenteeism from work due to illness may be reduced by one of several ways. First, the ill employee may make up the lost production when he or she returns to work from sick leave. Second, coworkers may help make up the lost production by sharing the ill employee's responsibilities. Third, when the economy is not at full employment, the employer may be able to find a replacement worker at little additional cost.
Based on these arguments, we analyzed another scenario in which we assumed the value of lost earnings was half of that in the base-case scenario (scenario E). The estimated effect of depression treatment on net economic costs in this scenario was $17 (p=.9). Even in this conservative scenario, depression treatment still paid for itself.