Objective: There has been debate whether polymorphisms within the serotonin transporter-linked polymorphic region (5-HTTLPR) moderate susceptibility to posttraumatic stress disorder (PTSD). The authors investigated 5-HTTLPR genotypes and their interaction with the number of traumatic events in the prediction of PTSD in a general population sample. Method: Analyses were based on data from 3,045 subjects who participated in the Study of Health in Pomerania. All participants were assessed with the PTSD module of the Structured Clinical Interview for DSM–IV. The short (S)/long (L) polymorphism of 5-HTTLPR (rs4795541) and the A-G polymorphism (rs25531) were genotyped. Results: Among the participants, 1,663 had been exposed to at least one traumatic event, and 67 (4.0%) developed PTSD. Among those who had experienced less than three traumatic events, the lifetime prevalence of PTSD was 2.6%, 3.5%, and 4.3% for those with zero, one, and two L A alleles, respectively, but the lifetime prevalence was 0%, 7.3%, and 19.6%, respectively, among those with three or more traumatic experiences. This finding suggests that there is an additive excess risk for frequent trauma in the L A /L A genotype, which was confirmed by the relative excess risk due to interaction (RERI). In allelic analysis, RERI was 3.3. Thus, the odds ratio for PTSD in L A allele carriers exposed to three or more traumas was 3.3 times higher as a result of the interaction between PTSD and the L A allele. Conclusions: An additive gene-environment interaction with the high expression L A allele of 5-HTTLPR and frequent trauma in PTSD was found. The attributable proportion indicated that more than 60% of all L A allele carriers who were exposed to three or more traumas developed PTSD as a result of an interaction between genotype and exposure.
Since the introduction of posttraumatic stress disorder (PTSD) as a diagnosis in DSM–III (1), PTSD has been recognized as a major issue in public health (2, 3) . PTSD is characterized by distressing and/or impairing symptoms that occur after experiencing, witnessing, or being confronted with a traumatic event that includes an actual or perceived threat to the self or others (4) . The disorder involves repeated and intrusive memories related to the trauma, avoidance of trauma-related stimuli, and hyperarousal (4) .
Although the majority of individuals exposed to traumatic stress will experience some kind of transient distress, only a minority will develop PTSD (5, 6) . Genetic factors have been shown to explain a relevant proportion of the variance of PTSD and are assumed to moderate the vulnerability to the adverse effects of traumatic stress (7) . To date, very few studies have addressed the issue of genetic vulnerability to PTSD (8 – 10) . There is evidence that the short (S) allele of the serotonin transporter-linked polymorphic region (5-HTTLPR) is associated with an increased sensitivity for anxiety (11) and depression (12 – 14) when a person is exposed to stressful life events. In addition, an association between the S allele and an increased reactivity of the amygdala was found in healthy subjects (15, 16) . Thus, the 5-HTTLPR constitutes a genetic candidate region that may modulate emotional responses to traumatic events and thereby influence the risk for the development of PTSD. One Korean study (17) found an association of the 5-HTTLPR gene with PTSD in a clinical population. Recently, Kilpatrick et al. (18) investigated a posthurricane population in Florida (N=589), with 19 subjects (3.2%) suffering from posthurricane PTSD. Kilpatrick et al. reported an interaction among the following variables: high hurricane exposure, low social support, and the S/S genotype of the 5-HTTLPR. No direct gene effects on PTSD or two-way interactions were found. Given the small number of subjects with PTSD in the Kilpatrick et al. study and the fact that the genotype only became statistically significant at the level of three-way interaction, these results should be regarded with caution.
Based on meta-analyses and power simulation on gene-by-environment interaction studies in depression, Munafo et al. (14) concluded that findings implicating the S allele of the 5-HTTLPR could have occurred by chance alone. Munafo et al. pointed to the need for more rigorous methodological approaches in gene-by-environment research.
In light of these limitations of the research thus far, the objective of our general population study of 3,045 community residents was twofold. We aimed to 1) investigate the direct effects of 5-HTTLPR on PTSD and 2) assess gene-by-environment effects, following an approach proposed by several experts (19 – 23) to examine possible biological interactions. We used the number of traumatic events as a quantitative environmental exposure variable because the number of traumatic events can be considered an approximation to the individual severity of exposure. Accordingly, higher numbers of traumatic events have been associated with an increased risk of subsequent PTSD (24) .
Method
General Population Sample
In the present study, data from the Study of Health in Pomerania were used (13, 25, 26) . The target population was made up of adult German residents (age range: 20 to 79 years old) residing in Northeastern Germany in three cities and 29 communities, with a total population of 212,157. The total number of eligible participants in the sample was 6,267. Of these, 4,310 Caucasian subjects participated in the Study of Health in Pomerania–0 (1997–2001). Follow-up examination (Study of Health in Pomerania–1) was conducted 5 years after baseline, and 3,300 subjects were assessed. All participants gave written informed consent. The study was approved by the local Institutional Review Board and conformed to the principles of the Declaration of Helsinki. Complete sociodemographic and psychometric data as well as the 5-HTTLPR genotypes were available from 3,045 subjects from the Study of Health in Pomerania–1.
Interview and Psychometric Assessments
The health-related interview of the Study of Health in Pomerania–1 involved the PTSD module of the Structured Clinical Interview for DSM-IV (SCID) (27), the Mini-Mental State Examination (28), and the Composite International Diagnostic–Screener (29) .
The PTSD module of the SCID (27) was used to assess trauma exposure and PTSD. The following traumatic events were assessed: combat or war zone experience, physical assault, rape, childhood sexual abuse, natural disaster, serious or nearly fatal accident, imprisonment and/or torture, life-threatening illness, sudden and unexpected death of a loved one, and witnessing or learning about traumas experienced by others. If a participant answered “no” to each of the trauma questions, the module was terminated. In the event of trauma exposure, the interview was continued, assessing DSM-IV PTSD symptoms, including criterion A2 (experiencing high distress during/after the event), criterion B (five re-experiencing symptoms), criterion C (seven avoidance symptoms), and criterion D (five arousal symptoms). For the diagnosis of PTSD to be determined, we required at least one symptom of re-experiencing, three avoidance symptoms, and two symptoms of hyperarousal. If participants did not pass the required diagnostic threshold (e.g., at least one re-experiencing symptom), the interview was terminated.
Depression that occurred during the 12 months prior to the examination was assessed by face-to-face interview using the Composite International Diagnostic–Screener (29) . The screening questions for depressive disorders, according to DSM-IV, were as follows: “feelings of sadness or depressed mood for a period of at least 2 weeks” and “lack of interest, tiredness, or loss of energy for a period of at least 2 weeks.” If both items were endorsed, we assigned the label “depression at the syndrome level.” Based on the Mini-Mental State Examination score (28), subjects were classified as low (Mini-Mental State Examination score <23) or high (Mini-Mental State Examination score ≥23) scoring. This variable was used to adjust for cognitive decline in some older participants.
Genotyping of the 5-HTTLPR
The SLC6A4 gene harbors a variable number tandem repeat polymorphism in the transcription control region of the gene that is located approximately 1 kb upstream from the transcription initiation site. This area has been associated with differential expression of the transporter (rs4795541) (30) . Both variants (S and long [L]) differ by a 43 base pair insertion/deletion. Within the inserted fragment, an additional common single nucleotide polymorphism (SNP) occurs (rs25531) and has been reported to further affect the transcriptional activity of the SLC6A4 promoter by the genotype-dependent generation of an AP2 transcription factor binding site in the rs25531 G allele (31) . Together, this leads to the thought that 5-HTTLPR is triallelic with the following alleles: S, L A, and L G .
We developed a restriction fragment length polymorphism method that allows for determination of both variants (S/L; rs25531) within one assay. The 5-HTTLPR region was polymerase chain reaction amplified using the oligonucleotide primers SLC6A4_SE (5′-CTCCTAGGATCGCTCCTGCATC-3′) and SLC6A4_AS (5′-GGACCGCAAGGTGG-GCGGGAGGCTTGGAG-3′), resulting in amplicons of 294 base pairs for the S variant and 337 base pairs for the L variant. The restriction enzyme BcnI (Fermentas) digested the rs25531 variant differentially, in addition to two constitutive restriction sites in the amplicon. This resulted in the following fragments: 200, 61, and 33 base pairs for the S allele; 243, 61, and 33 base pairs for the L A allele; and 70, 173, 61, and 33 base pairs for the L G allele. The detection of fragments of 173, 200, and 243 base pairs in 4% agarose gels allowed for allocation to the respective alleles. Representative samples of different genotypes were further verified by sequencing of the amplicons. Based on previous reports on gene expression, we classified the genotypes into the following three functional “triallelic” genotypes: L A /L A ; L G /L A or S/L A ; and L G /L G or L G /S or S/S (18, 31) .
The main analyses were repeated using the classical “biallelic” classification without separating L G from L A (see the data supplement accompanying the online version of this article).
Statistical Analyses
Comparisons between groups were performed using Mann-Whitney U tests (continuous data) and unadjusted logistic regression (nominal data). The Cochran-Armitage Trend Test was used to determine an additive mode of inheritance. Criteria B, C, and D were dichotomized into present (≥1 positive item) or absent (0 items). The analysis of direct gene effects between the triallelic genotypes and the diagnosis of PTSD was performed using logistic regression.
To assess gene-environment interaction using the crude prevalence of lifetime PTSD, we used tables with three genotype categories crossed with two levels of trauma frequency (19, 20) . The number of traumatic events was dichotomized (<2/≥2 events, <3/≥3 events, and <4/≥4 events) and analyzed in separate regression models. Estimated absolute risks, odds ratios, and 95% confidence intervals (CIs) were calculated for the resulting six-by-two tables. In several cases, conventional maximum likelihood estimations for the dichotomized outcome were potentially biased as a result of an expected cell count <5. We examined this situation in three ways. First, based on the bootstrap approach, robust estimates were calculated as described in the present article. In any instance in which there was a genotype-trauma combination with no cases of PTSD, median-unbiased estimates were used. Second, odds ratios and CIs were alternatively estimated using a semi-Bayes approach (32) . The posterior approximations were derived from an ordinary logistic regression (32) . Third, the number of symptoms for criterion D was regressed in a count model (negative binomial regression).
Genotype differences in susceptibility to trauma were estimated by biological interaction, which is measured by departure from an additive model (22) . For the quantification of the magnitude of an interaction effect, the relative excess risk due to interaction (RERI) was calculated. To clarify this, we computed the crude absolute PTSD prevalence for each category and then the absolute excess risk due to additive interaction as well as the corresponding crude RERI. It is not straightforward to compute the adjusted absolute excess risk in logistic regression. However, the adjusted RERI is easily estimated using the following basic formula for RERI (22) (OR=odds ratio):
RERI=OR risk allele and high trauma –OR risk allele and low trauma –OR no risk allele and high trauma +1
Additionally, the proportion of disease among subjects with both exposures (traumatic events ≥3 and at least one L A allele) that was attributable to their interaction (attributable proportion) was calculated for two dichotomous determinants as follows (22) (AP=attributable proportion):
AP=RERI/OR risk allele and high trauma
As recommended (22), the coding was chosen in such a manner that in the presence of additive interaction, both RERI and attributable proportion were greater than zero; whereas in the absence of interaction, both RERI and attributable proportion were equal to zero. If the 95% CI excluded zero, then the p value for the interaction was significant (p<0.05). A bias-corrected and accelerated bootstrap approach (10,000 bootstrap samples) was applied in order to yield the CI of RERI and attributable proportion (19, 21) . RERI and attributable proportion were calculated for an allelic model (L A versus L G /S), a dichotomized model (zero or one versus two L A alleles), and a continuous genetic model (zero, one, or two L A alleles).
All analyses were performed as unadjusted (crude), as adjusted for age (10-year age groups [20s, 30s, 40s, etc.]) and gender, and as “fully adjusted” models, including low (<23) Mini-Mental State Examination scores (yes/no) and depression within the last 12 months (yes/no). Analyses were performed with STATA/SE software, version 10.1 (StataCorp LP, College Station, Tex.). Power analyses were performed using the program POWER (33) .
Results
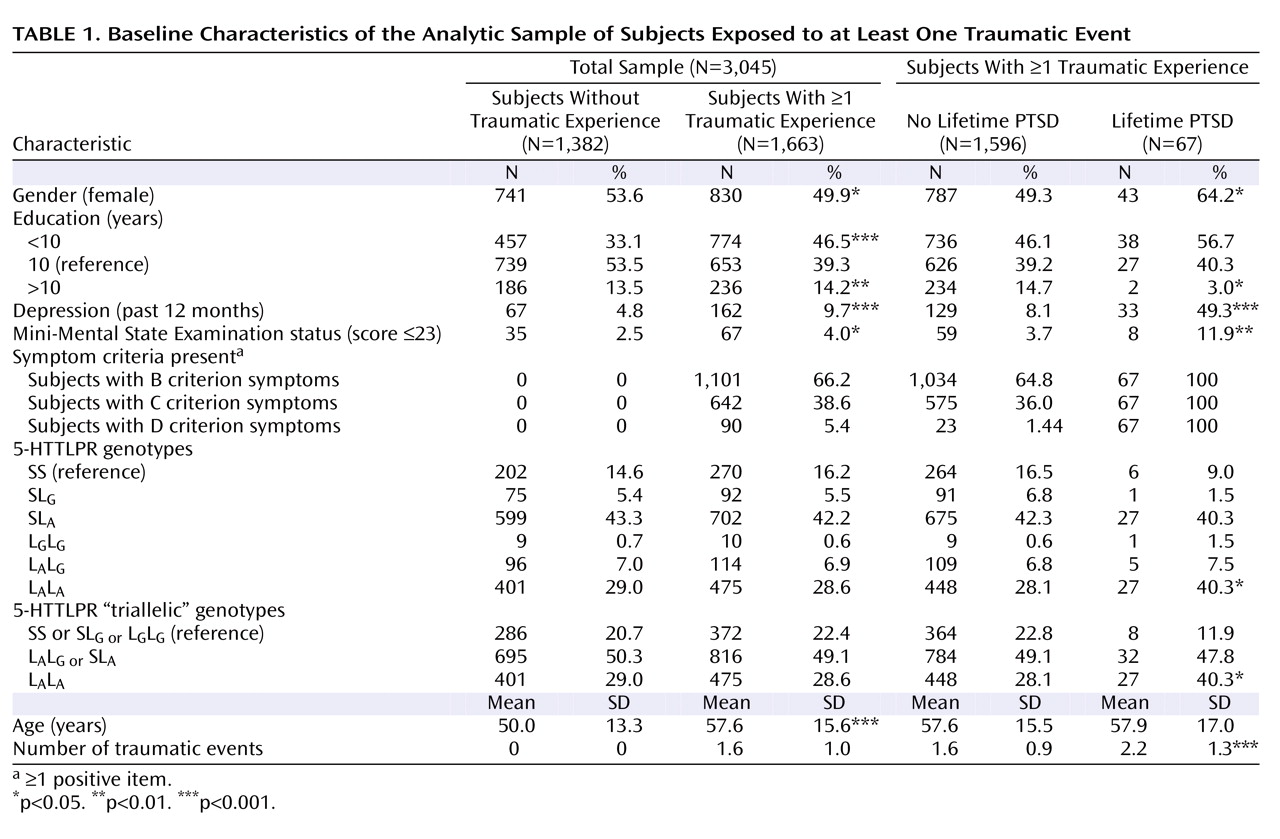
The description of clinical and demographic characteristics of the sample is provided in Table 1 . There was no departure from the Hardy-Weinberg equilibrium (total sample [triallelic]: χ 2 =2.53, df=2, p=0.28; exposed sample [triallelic]: χ 2 =1.18, df=2, p=0.55). All genetic analyses were based on 1,663 subjects who reported exposure to at least one traumatic event. Sixty-seven subjects (4.03%) met the diagnostic criteria for lifetime diagnosis of PTSD. There were no associations between the number of traumatic events and the triallelic genotypes (F=0.115, df=2, 1660, p=0.89).
Gene Main Effects
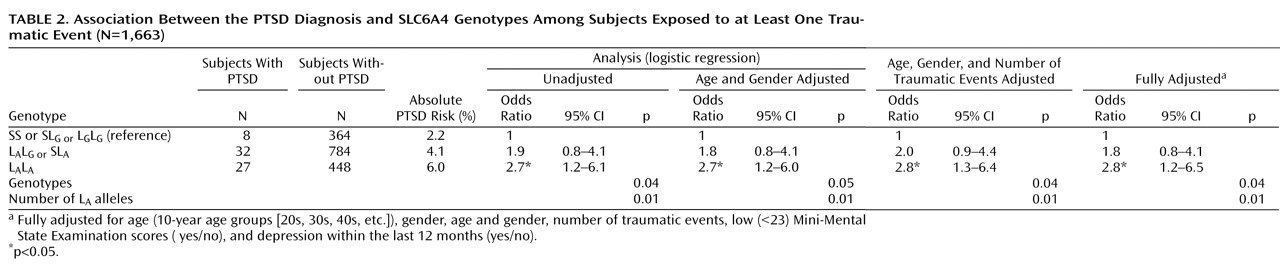
Main effects of the three genotypes with the diagnosis of PTSD (L A /L A ; L G /L A or S/L A ; and L G /L G or L G /S or S/S) were analyzed by logistic regression analysis ( Table 2 ). All associations between the L A /L A genotype and PTSD (both crude and adjusted) were statistically significant. There was clear evidence for a dose-response relationship, since among subjects with zero, one, and two L A alleles the crude proportion of PTSD increased from 2% to 4% and 6%, respectively. The Cochran-Armitage test indicated a clear additive mode for L A alleles (χ 2 =6.78, df=1, p=0.009), with no departure from linearity (χ 2 =0.00, df=1, p=0.99). The allelic analyses revealed an effect for the L A allele (odds ratio=1.6; 95% CI=1.1–2.4) but not for the more rare L G allele (odds ratio=0.7; 95% CI=0.3–1.6) on PTSD in the fully adjusted model (see the data supplement accompanying the online version of this article). No associations were established between the 5-HTTLPR genotypes and criteria B, C, or D (p≥0.05).
Gene-Environment Interaction
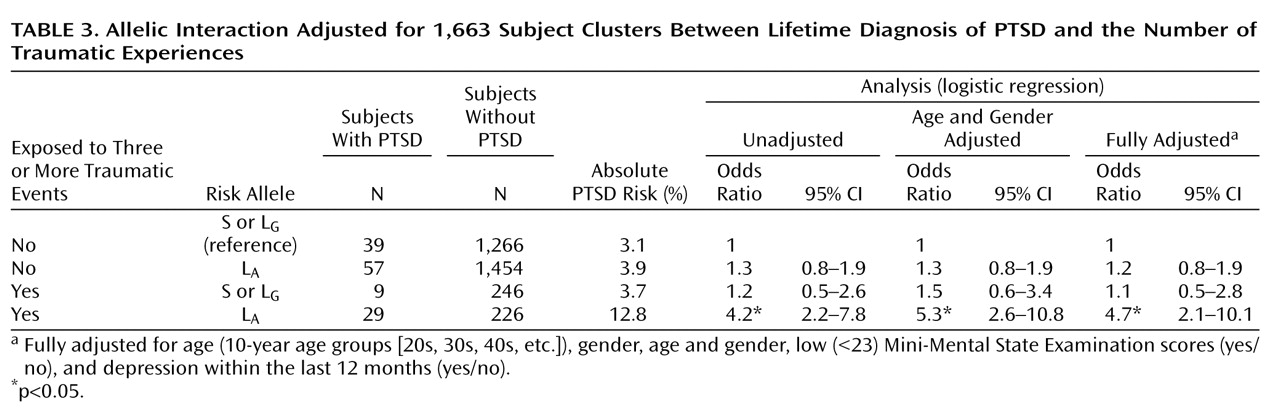
In allelic analyses, the estimated absolute risk among subjects who were not exposed to three or more traumatic events was 3.1% for those without the L A allele and 3.9% for those with the L A allele; whereas the risk among subjects who were exposed to three or more traumatic events was 3.7% for those without the L A allele but 12.8% for those with the L A allele ( Table 3 ). Thus, based on the same difference in absolute risks for the L A allele in trauma-exposed and nonexposed subjects, the absolute additive excess risk for trauma-exposed subjects with the L A allele was as follows: 12.8%–3.7%–3.9%+3.1%=8.3%. The unadjusted RERI was then 8.3%/3.1%=2.7, which is in terms of the odds ratio equivalent to 2.7=4.2–1.2–1.3+1 ( Table 3 ). Thus, the unadjusted odds ratio of having the lifetime diagnosis of PTSD among subjects with ≥3 traumas and the L A allele relative to those without the L A allele was 2.7 times higher than the condition in which no interaction between traumas and the L A allele was present (e.g., absolute risk of 4.5% instead of 12.8% or, equivalently, odds ratio=4.5/3.1=1.5 instead of odds ratio=4.2). For the final model, RERI was 3.3 (95% CI=1.2–8.2 [ Table 4 ]). Importantly, RERI–1>0 holds for the 95% CI. The unadjusted attributable proportion was 2.7/4.2=0.64 (64%), and the fully adjusted attributable proportion was 71% (95% CI=41–88), meaning that approximately 71% of PTSD diagnoses among subjects with ≥3 traumas and the L A allele was attributable to the interaction between the two.
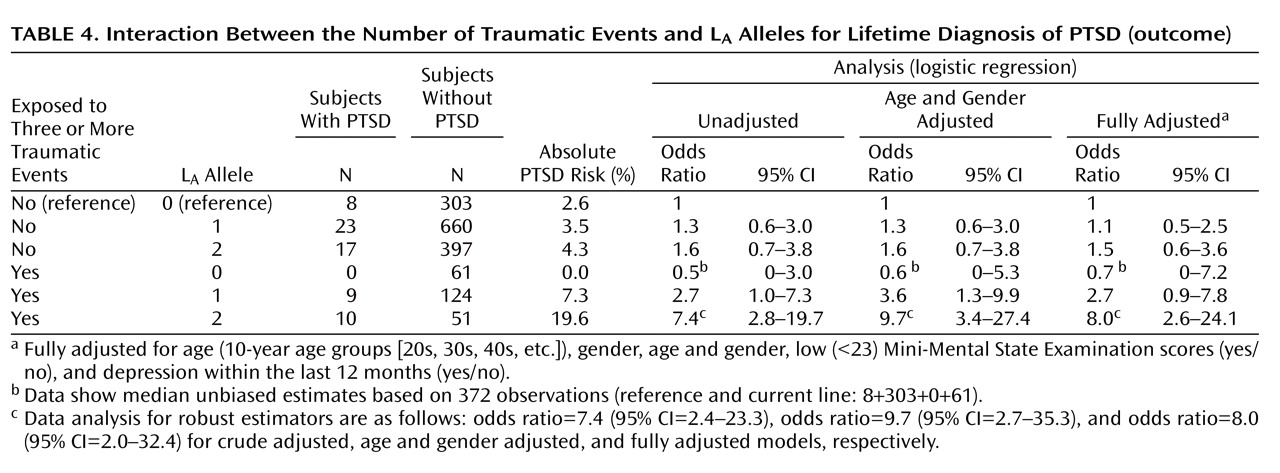
To avoid a sparse data problem, referring to a genotype-trauma combination with no cases of PTSD ( Table 4 ), subjects with zero or one L A allele were grouped into one category versus subjects with two L A alleles. The absolute risks were 31/963=3.2% and 4.3% among nonexposed subjects without and with two L A alleles, respectively, and 9/185=4.9% and 19.6% among exposed subjects without and with two L A alleles, respectively ( Table 4 ). This type of RERI was crude (13.6%/3.2%=4.25) and fully adjusted (5.5) (95% CI=0.8–18.3, p<0.05). The unadjusted attributable proportion was 4.25/(10×963/[31×51])=4.25/6.1=0.70 (70%), and the fully adjusted attributable proportion was 74% (95% CI=18–92).
Since the allelic analyses supported that subjects with only one L A allele possibly had a higher risk for PTSD when trauma exposed compared with those subjects carrying no L A alleles, we calculated RERI for the number of L A alleles as a continuous variable. This type of RERI directly estimates the relative excess risk for one L A allele compared with no L A alleles. In the present study, RERI was 1.3 for the unadjusted model and 1.5 (95% CI=0.5–4.3, p<0.05) for the fully adjusted model ( Table 4 ). This means that among subjects with ≥3 traumas the odds ratio of having PTSD was 1.5 times higher with one L A allele compared with the absence of interaction between the L A alleles and traumas. We confirmed these results using a Bayesian approach to address the sparse data problem (see the data supplement accompanying the online version of this article). Prior limits similar to the related CIs of the fully adjusted model for the number of symptoms from the D criterion were utilized (see the data supplement accompanying the online version of this article).
When four instead of three was used as a cutoff point for the number of traumas, RERI for the dichotomized genotype (zero or one L A allele versus two L A alleles) increased to 8.8 (95% CI=1.6–31.7, p<0.05) and attributable proportion increased to 86% (95% CI=33–97). Given the lower number of subjects with ≥4 traumatic events, the continuous models were less robust. When two was used as a cutoff point for the number of traumas, no statistically significant interactions emerged.
For the number of symptoms from the D criterion as the outcome (see the data supplement accompanying the online version of this article), no genotype-trauma combination with a zero count occurred. RERI for the continuous genetic model (zero, one, or two L A alleles) was 1.2 (95% CI=0.5–2.8, p<0.05) and attributable proportion for the continuous genetic model was 72% (95% CI=23–126). No statistically significant interactions emerged when performing the analyses for B and C criteria irrespective of the trauma threshold.
Discussion
Our results demonstrate a clear gene main effect, with an additive relationship between the number of L A alleles and the diagnosis of PTSD in community residents exposed to at least one traumatic event. The specificity of the “gain-of-function” L A allele compared with the L G allele on PTSD could be shown in the allelic analyses, since the effect of the L G allele was not different from that of the S allele (see the data supplement accompanying the online version of this article). Further, significant gene-by-environment interactions with moderate CIs between the L A alleles and the number of traumatic events on the manifestation of PTSD were established for ³3 traumatic events. These interaction effects could already be shown in carriers of one L A allele (versus zero L A alleles) but were much stronger in carriers of two L A alleles. The proportion of subjects with PTSD among those with both exposures (traumatic events ≥3 and at least one L A allele) that was attributable to the interaction between traumatic events (<3 events/≥3 events) and the L A alleles ranged from 61% to 74%, depending on the model. Since RERI–1>0 holds for the allelic analysis, a stronger condition than RERI>0 was met and a causal synergistic action may be assumed (34) .
The 5-HTTLPR was not associated directly or through interaction with re-experiencing (criterion B) or avoidance behavior (criterion C). However, for the D criterion (hyperarousal), gene-by-environment effects were found. Since most subjects with the D criterion symptom also fulfilled the diagnosis of PTSD, we are unsure whether the association between the L A alleles and hyperarousal was specific or emerged from the overlap with PTSD.
Our results of the increased susceptibility for PTSD in carriers of the L A allele contradict other clinical and neurobiological findings that found the S allele to be associated with a higher susceptibility to anxiety and depression (12, 13, 18) . However, many findings on the neurobiological function of the 5-HTTLPR were derived from cell cultures and animal models and have not been validated in humans (35) . Some functional magnetic resonance imaging (fMRI) studies found an increased amygdala reactivity to fearful stimuli in healthy subjects carrying the S allele (15, 16) . In contrast, a recent fMRI study in adolescents suffering from anxiety and depression found the L A /L A genotype to be associated with increased amygdala reactivity, whereas healthy adolescents showed an increased amygdala response when carrying the S(L G ) allele (36) . This points to a putative differential neurobiological effect of the L A versus the S(L G ) allele, depending on the psychobiological background of the probands.
Interestingly, obsessive-compulsive disorder (OCD) has recently been associated with “gain-of-function” polymorphisms of the L allele that increase the transcription of the serotonin transporter (31, 37) . OCD shares psychopathological features with PTSD, such as conditioned fear, intrusive thoughts, avoidance behavior, and increased emotional and physiological arousal (38) . A reduced synaptic availability of serotonin as a result of an increased reuptake might represent a risk factor for decreased prefrontal control over disinhibited subcortical circuits in PTSD and OCD (39, 40) .
Our findings contradict the results of Kilpatrick et al. (18), which emphasized the problem of statistical power. Modeling the 80% power (p<0.05, two-sided) of a direct gene effect for our exposed sample, the detection of an odds ratio as low as 1.65 per L A allele was feasible with 80% power in our sample. In contrast, in the study conducted by Kilpatrick et al. (18) the power was <50% for an effect size as low as 1.65 per S allele. Moreover, power simulations for the additive gene-by-environment effects in our sample demonstrated 76% power for a RERI=4 for the dichotomized model (L A /L A versus all other genotypes) (see the data supplement accompanying the online version of this article). In fact, we even found a RERI=5.5 in our analyses. Therefore, it is rather unlikely that the direct and gene-by-environment effects in our study occurred by chance.
Lee et al. (17) reported an association of the S allele with PTSD in patients in Korea. However, PTSD in clinical samples may be confounded by a high degree of comorbid psychopathology, and selection bias may occur through treatment seeking behavior. Moreover, the allele distribution of the S/L polymorphism in Asians is reversed relative to Caucasians. Further, Lee et al. (17) did not analyze the gain-of-function polymorphism rs25531. Thus, the validity of their results is limited, especially in Caucasian samples.
Limitations of the Study
In the present study, we cannot exclude the possibility that subjects with a high symptom load or PTSD had recall biases (i.e., subjects who reported more traumatic events in the past than those without PTSD or who reported fewer events because they only recalled the most severe traumatic events in the past). This misclassification is differential, and the direction of bias is unknown. However, we used a validated questionnaire in order to reduce the recall bias (27) . Although the number of subjects with PTSD (N=67) was three times larger than that of the Kilpatrick et al. study and our power analyses demonstrated a robust statistical power, we still have to acknowledge that the sample size in our study was limited.
In addition to the number of traumatic events, the type of trauma may influence the risk for PTSD (24) . Therefore, in replication studies, qualitative trauma-related variables should be investigated as well.
Footnotes
Received Oct. 17, 2008; revisions received Dec. 19, 2008, and March 10, 2009; accepted March 23, 2009 (doi: 10.1176/appi.ajp.2009.08101542). From the Department of Psychiatry and Psychotherapy, University of Greifswald, Germany; Department of Psychosomatic Medicine and Psychotherapy, University of Hamburg, Germany; Institute of Epidemiology and Social Medicine, University of Greifswald, Germany; Institute of Pharmacology, University Hospital, Ernst-Moritz-Arndt University, Greifswald, Germany; Institute of Clinical Psychology, University of Heidelberg, Germany; Department of Internal Medicine A, University of Greifswald, Germany; Institute for Community Medicine, University of Greifswald, Germany. Address correspondence and reprint requests to Dr. Grabe, Department of Psychiatry, Ernst-Moritz-Arndt-University of Greifswald, HANSE-Klinikum Stralsund, Rostocker Chaussee 70, 18437 Stralsund, Germany; [email protected] (e-mail).
Dr. Grabe has received funding from the German Research Foundation and Federal Ministry of Education and Research Germany; he has received speaker’s honoraria from Bristol-Myers Squibb, Eli Lilly, Novartis, Eisai, and Wyeth; he has received travel funds from Janssen-Cilag and Eli Lilly; and he has received funding from the SALUS-Institute for Trend-Research and Therapy Evaluation in Mental Health. Dr. Spitzer has received travel funds and a speaker’s honorarium from Janssen-Cilag; and he has received a research grant from the “Stiftung zur Aufarbeitung der SED-Diktatur.” Dr. Barnow has received funding from the German Research Foundation and Federal Ministry of Health Germany. Dr. Lucht has received funding from the German Research Foundation and Federal Ministry of Education and Research; and he has received speaker’s honoraria from Sanofi-Aventis, Eli Lilly, and Sanofi-Synthelabo. Dr. Freyberger has received funding from the German Research Foundation, Social Ministry of the Federal State of Mecklenburg-West Pomerania of Germany, and Family Ministry of the Federal Republic of Germany; he has received speaker’s honoraria from AstraZeneca, Eli Lilly, and Novartis; and he has received travel funds from Janssen-Cilag. Dr. John has received funding from the German Research Foundation, German Cancer Aid, European Union, Federal Ministry of Education and Research Germany, and Social Ministry of the Federal State of Mecklenburg-West Pomerania of Germany. Dr. Wallaschofski has received research grants from Pfizer, Novartis, Novo Nordisc, Sanofi-Aventis, and the German Research Foundation. Dr. Völzke has received research grants from Sanofi-Aventis, Biotronik, the Humboldt Foundation, the Federal Ministry of Education and Research (Germany), and the German Research Foundation. Dr. Rosskopf has received research grants from the Federal Ministry of Education and Research and the State Ministry of Education and Research. Dr. Schwahn, Ms. Marcinek, and Ms. Frahnow report no competing interests.
The present study is part of the Community Medicine Research net of the University of Greifswald, Germany, which is funded by the Federal Ministry of Education and Research (grants 01ZZ9603 and 01ZZ0103), the Ministry of Cultural Affairs, and the Social Ministry of the Federal State of Mecklenburg-West Pomerania. The study was partially funded by the German Research Foundation (DFG: GR 1912/5–1).
The authors thank David R. Jacobs (University of Minnesota) for advice on the presentation of the complex results.
References
1.
American Psychiatric Association: Diagnostic and Statistical Manual of Mental Disorders, 3rd ed. Washington, DC, American Psychiatric Publishing, 1980
Galea S, Ahern J, Resnick H, Kilpatrick D, Bucuvalas M, Gold J, Vlahov D: Psychological sequelae of the Sept 11 terrorist attacks in New York City. N Engl J Med 2002; 346:982–987
Norris FH, Elrod CL: Psychosocial consequences of disaster: a review of past research, in Methods for Disaster Mental Health Research. Edited by Norris FH, Galea S, Friedman MJ, Watson PJ. New York, Guilford, 2006, pp 20–42
Stein MB, Jang KL, Taylor S, Vernon PA, Livesley WJ: Genetic and environmental influences on trauma exposure and posttraumatic stress disorder symptoms: a twin study. Am J Psychiatry 2002; 159:1675–1681
Binder EB, Bradley RG, Liu W, Epstein MP, Deveau TC, Mercer KB, Tang Y, Gillespie CF, Heim CM, Nemeroff CB, Schwartz AC, Cubells JF, Ressler KJ: Association of FKBP5 polymorphisms and childhood abuse with risk of posttraumatic stress disorder symptoms in adults. JAMA 2008; 299:1291–1305
Caspi A, Sugden K, Moffitt TE, Taylor A, Craig IW, Harrington H, McClay J, Mill J, Martin J, Braithwaite A, Poulton R: Influence of life stress on depression: moderation by a polymorphism in the 5-HTT gene. Science 2003; 301:386–389
Grabe HJ, Lange M, Wolff B, Volzke H, Lucht M, Freyberger HJ, John U, Cascorbi I: Mental and physical distress is modulated by a polymorphism in the 5-HT transporter gene interacting with social stressors and chronic disease burden. Mol Psychiatry 2005; 10:220–224
Hariri AR, Mattay VS, Tessitore A, Kolachana B, Fera F, Goldman D, Egan MF, Weinberger DR: Serotonin transporter genetic variation and the response of the human amygdala. Science 2002; 297:400–403
Lee HJ, Lee MS, Kang RH, Kim H, Kim SD, Kee BS, Kim YH, Kim YK, Kim JB, Yeon BK, Ohio KS, Ohio BH, Yoon JS, Lee C, Jung HY, Chee IS, Paik IH: Influence of the serotonin transporter promoter gene polymorphism on susceptibility to posttraumatic stress disorder. Depress Anxiety 2005; 21:135–139
Kilpatrick DG, Koenen KC, Ruggiero KJ, Acierno R, Galea S, Resnick HS, Roitzsch J, Boyle J, Gelernter J: The serotonin transporter genotype and social support and moderation of posttraumatic stress disorder and depression in hurricane-exposed adults. Am J Psychiatry 2007; 164:1693–1699
Botto LD, Khoury MJ: Commentary: facing the challenge of gene-environment interaction: the two-by-four table and beyond. Am J Epidemiol 2001; 153:1016–1020
Knol MJ, van der Tweel I, Grobbee DE, Numans ME, Geerlings MI: Estimating interaction on an additive scale between continuous determinants in a logistic regression model. Int J Epidemiol 2007; 36:1111–1118
Vandenbroucke JP, von Elm E, Altman DG, Gotzsche PC, Mulrow CD, Pocock SJ, Poole C, Schlesselman JJ, Egger M: Strengthening the Reporting of Observational Studies in Epidemiology (STROBE): explanation and elaboration. Ann Intern Med 2007; 147:W163–W194
Darves-Bornoz JM, Alonso J, de Girolamo G, de Graaf R, Haro JM, Kovess-Masfety V, Lepine JP, Nachbaur G, Negre-Pages L, Vilagut G, Gasquet I; ESEMeD/MHEDEA 2000 Investigators: Main traumatic events in Europe: PTSD in the European study of the epidemiology of mental disorders survey. J Trauma Stress 2008; 21:455–462
John U, Greiner B, Hensel E, Ludemann J, Piek M, Sauer S, Adam C, Born G, Alte D, Greiser E, Haertel U, Hense HW, Haerting J, Willich S, Kessler C: Study of Health in Pomerania (SHIP): a health examination survey in an East German region: objectives and design. Soz Praventivmed 2001; 46:186–194
Spitzer C, Barnow S, Volzke H, John U, Freyberger HJ, Grabe HJ: Trauma and posttraumatic stress disorder in the elderly: findings from a German community study. J Clin Psychiatry 2008; 69:693–700
First MB, Spitzer RL, Gibbon M, Williams JB: Structured Clinical Interview for DSM-IV Axis I Disorders. Washington, DC, American Psychiatric Publishing, 1997
Folstein MF, Folstein SE, McHugh PR: Mini-Mental State: a practical method for grading the cognitive state of patients for the clinician. J Psychiatr Res 1975; 12:189–198
Wittchen H, Höfler M, Gander F, Pfister H, Storz S, Üstün B, Müller N, Kessler RC: Screening for mental disorders: performance of the Composite International Diagnostic–Screener (CID–S). Int J Methods Psychiatr Res 1999; 8:59–70
Heils A, Teufel A, Petri S, Seemann M, Bengel D, Balling U, Riederer P, Lesch KP: Functional promoter and polyadenylation site mapping of the human serotonin (5-HT) transporter gene. J Neural Transm Gen Sect 1995; 102:247–254
Garcia-Closas M, Lubin JH: Power and sample size calculations in case-control studies of gene-environment interactions: comments on different approaches. Am J Epidemiol 1999; 149:689–692
Murphy DL, Fox MA, Timpano KR, Moya P, Ren-Patterson R, Andrews AM, Holmes A, Lesch KP, Wendland JR: How the serotonin story is being rewritten by new gene-based discoveries principally related to SLC6A4, the serotonin transporter gene, which functions to influence all cellular serotonin systems. Neuropharmacology 2008; 55:932–960
Lau JY, Goldman D, Buzas B, Fromm SJ, Guyer AE, Hodgkinson C, Monk CS, Nelson EE, Shen PH, Pine DS, Ernst M: Amygdala function and 5-HTT gene variants in adolescent anxiety and major depressive disorder. Biol Psychiatry 2009; 65:349–355
Berkowitz RL, Coplan JD, Reddy DP, Gorman JM: The human dimension: how the prefrontal cortex modulates the subcortical fear response. Rev Neurosci 2007; 18:191–207
If you have the appropriate software installed, you can download article citation data to the citation manager of your choice. Simply select your manager software from the list below and click Download.
For more information or tips please see 'Downloading to a citation manager' in the Help menu.
PsychiatryOnline subscription options offer access to the DSM-5-TR® library, books, journals, CME, and patient resources. This all-in-one virtual library provides psychiatrists and mental health professionals with key resources for diagnosis, treatment, research, and professional development.
Need more help? PsychiatryOnline Customer Service may be reached by emailing [email protected] or by calling 800-368-5777 (in the U.S.) or 703-907-7322 (outside the U.S.).
If the address matches an existing account you will receive an email with instructions to retrieve your username
Create a new account
Change Password
Password Changed Successfully
Your password has been changed
Login
Reset password
Can't sign in? Forgot your password?
Enter your email address below and we will send you the reset instructions
If the address matches an existing account you will receive an email with instructions to reset your password.
Change Password
Congrats!
Your Phone has been verified
×
As described within the American Psychiatric Association (APA)'s Privacy Policy and Terms of Use, this website utilizes cookies, including for the purpose of offering an optimal online experience and services tailored to your preferences. Please read the entire Privacy Policy and Terms of Use. By closing this message, browsing this website, continuing the navigation, or otherwise continuing to use the APA's websites, you confirm that you understand and accept the terms of the Privacy Policy and Terms of Use, including the utilization of cookies.
