Designing Case-Control Studies: Decisions About the Controls
Publication: American Journal of Psychiatry
Abstract
The authors quantified, first, the effect of misclassified controls (i.e., individuals who are affected with the disease under study but who are classified as controls) on the ability of a case-control study to detect an association between a disease and a genetic marker, and second, the effect of leaving misclassified controls in the study, as opposed to removing them (thus decreasing sample size). The authors developed an informativeness measure of a study's ability to identify real differences between cases and controls. They then examined this measure's behavior when there are no misclassified controls, when there are misclassified controls, and when there were misclassified controls but they have been removed from the study. The results show that if, for example, 10% of controls are misclassified, the study's informativeness is reduced to approximately 81% of what it would have been in a sample with no misclassified controls, whereas if these misclassified controls are removed from the study, the informativeness is only reduced to about 90%, despite the reduced sample size. If 25% are misclassified, those figures become approximately 56% and 75%, respectively. Thus, leaving the misclassified controls in the control sample is worse than removing them altogether. Finally, the authors illustrate how insufficient power is not necessarily circumvented by having an unlimited number of controls. The formulas provided by the authors enable investigators to make rational decisions about removing misclassified controls or leaving them in.
[Introduction]
Epidemiologists developed case-control designs to aid them in searching for factors that might cause a given illness by comparing rates of exposure for potential risk factors in persons who have the illness (the case subjects) with those in the same population who presumably are not ill (the control subjects). The finding that people with lung cancer had higher rates of exposure to tobacco through their smoking than did controls who did not have lung cancer was the first evidence for the potential causative effects of smoking on cancer. Results of a case-control study are not considered as definitive as those of a randomized controlled trial, where a comparison is made prospectively between two identical populations, one exposed to the factor of interest and the other not, such as when Walter Reed exposed some soldiers to mosquitoes and placed others in a mosquito-free room to see if mosquitoes carried yellow fever. However, case-control studies are invaluable for several reasons: 1) many factors, such as patients' genotypes, cannot be assigned randomly; 2) several factors, such as genetic and environmental risks, can be examined simultaneously; and 3) case-control studies, in which subjects are observed once, generally cost less than a prospective randomized controlled trial. Investigators of mental disorders appropriately put much effort into defining caseness by rigorous diagnostic criteria. However, deciding who should be a control is equally important. In this article, as guidance for the investigator who intends to design such a study, we illustrate the consequences, for a study's results, of the decision to include or exclude from the control group persons who might have the targeted illness.
While it may seem obvious that control groups should include only disease-free subjects, several factors may induce investigators to consider unscreened controls. First, persons with illness are more likely to agree to participate in research than those without. Second, large databases of people who agreed to have their DNA anonymously genotyped with the results available for study already exist, which spares considerable expense for investigators. Third, without a definitive test for the absence of a targeted mental disorder, any claim that controls do not have the disorder seems limited in validity.
The psychiatric genetic literature contains ongoing discussions about the advantages and disadvantages of including affected individuals in control groups. For example, Tsuang et al. (1) noted that for relatively common conditions, one could reach different conclusions depending on whether one used screened controls or not; in their study of major depression, the morbid risk among relatives of controls was 8.1% when the controls came from the general population but 7.6% when only screened controls were used. Wickramaratne (2) showed that using population (i.e., unscreened) controls in a familial aggregation study did not affect validity (type I error) but did weaken statistical power. Moskvina et al. (3) have provided mathematical formulas for calculating power when unscreened controls are used.
In this article, we provide simple rules of thumb for evaluating the effect of misclassified disease-bearing controls on the ability of a case-control study to detect real differences between cases and controls. We also show that removing misclassified controls is better than leaving them in, even though doing so reduces total sample size. To do so, we consider case-control association studies between the disease and the genetic marker. We ask what happens when a specified proportion of the controls are misclassified. By “misclassified controls” we mean individuals who are classified as controls but who actually have the disease under study, that is, who should have been classified as cases. We then compare the strength of association one would get using the misclassified controls, as compared to using ideal controls.
Some investigators have proposed that using a very large number of controls can compensate for reduced power. It turns out, counterintuitively, that this is not true. We illustrate that beyond a certain point, collecting more and more controls does not improve a study's statistical ability to detect a true association in a case-control design.
Method
We assume an association study with a case-control design in which investigators are studying a possible association between a genetic marker—say, a single-nucleotide polymorphism—and a disease, with no comorbid conditions. We assume further that the case sample consists solely of correctly classified patients with the disease. However, the control sample may include some subjects who, unbeknownst to the investigator, are actually affected with the disease being studied. We refer to these subjects as “misclassified” controls.
We let p represent the true proportion of affected individuals who have the genetic marker in question, and q represents the same proportion among unaffected individuals. We assume that there is a true association between the disease and the genetic marker (i.e., p>q). Then we define α as the proportion of misclassified controls in the control sample; for example, an α of 0.10 means that 10% of individuals in the control sample actually have the disease, whereas an α of zero indicates that no one in the control sample has the disease.
As a measure of informativeness, we use the chi-square statistic as it would be calculated in a “perfect” sample. Say the true proportion of cases who have the genetic marker is 30%, and imagine a sample with 100 cases. Then, for the calculations in this article, we let exactly 30 of those individuals have the marker. (This is in contrast to a real-life sample, in which, because of sampling variation, one might observe only 26 of the 100 cases having the marker, or perhaps 33 of the 100.) Similar reasoning applies to the control sample.
Results
Below we give values of chi-square statistics for different association strengths and different proportions of misclassified controls. We then show how to interpret the tabular results, with examples. Next, we describe revealing patterns in the results and the useful rule of thumb we can derive from those patterns. Finally, we show what happens when the investigator can collect many controls but has no access to any more cases.
Numerical Results
We consider three situations:
•.
Situation 1: There are no misclassified controls—that is, no one in the control sample has the disease being studied. In this case, our measure of informativeness, the chi-square statistic, represents the gold standard for that sample size. We call this χ2CC (where CC stands for “correctly classified”).
•.
Situation 2: A proportion (α) of the controls in the sample are misclassified—that is, they actually have the disorder being studied. Now the χ2 statistic is reduced from the gold standard value of situation 1 to a lower value. We call this lower value χ2MC (“misclassified”).
•.
Situation 3: This is the same as situation 2, except that the investigator identifies and excludes the misclassified controls. Now the control sample is uniformly correctly classified again, but a price has been paid in terms of reduced size. The measure of informativeness for situation 3 is called χ2reduced.
Table 1 illustrates the behavior of all three types of χ2 for some representative values of p and q and for setups where the proportions of misclassified controls in the control sample are α=0.1 and α=0.25, respectively. We consider setups in which there are equal numbers of cases and controls (denoted by t=1, where t indicates the ratio of controls to cases) and setups in which there are twice as many controls as cases (t=2) in the sample. The table gives a “factor” for each combination of p, q, and α; the user multiplies that factor by the number of cases, N, to calculate the corresponding χ2.
| Values for q and χ2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| q=0.05 | q=0.10 | q=0.20 | |||||||
| Values for α, t, and p | χ2CC | χ2MC | χ2reduced | χ2CC | χ2MC | χ2reduced | χ2CC | χ2MC | χ2reduced |
| Misclassified controls, α=0.1 | |||||||||
| Equal Ns for controls and cases (t=1) | |||||||||
| p=0.1 | 0.0180 | 0.0142 | 0.0168 | ||||||
| p=0.2 | 0.1029 | 0.0793 | 0.0949 | 0.0392 | 0.0309 | 0.0366 | |||
| p=0.3 | 0.2165 | 0.1662 | 0.1992 | 0.1250 | 0.0976 | 0.1161 | 0.0267 | 0.0213 | 0.0251 |
| Twice as many controls as cases (t=2) | |||||||||
| p=0.1 | 0.0268 | 0.0207 | 0.0254 | ||||||
| p=0.2 | 0.1667 | 0.1241 | 0.1559 | 0.0577 | 0.0449 | 0.0548 | |||
| p=0.3 | 0.3606 | 0.2647 | 0.3351 | 0.1920 | 0.1463 | 0.1810 | 0.0373 | 0.0296 | 0.0357 |
| Misclassified controls, α=0.25 | |||||||||
| Equal Ns for controls and cases (t=1) | |||||||||
| p=0.1 | 0.0180 | 0.0094 | 0.0148 | ||||||
| p=0.2 | 0.1029 | 0.0514 | 0.0822 | 0.0392 | 0.0207 | 0.0324 | |||
| p=0.3 | 0.2165 | 0.1074 | 0.1721 | 0.1250 | 0.0645 | 0.1018 | 0.0267 | 0.0145 | 0.0224 |
| Twice as many controls as cases (t=2) | |||||||||
| p=0.1 | 0.0268 | 0.0135 | 0.0230 | ||||||
| p=0.2 | 0.1667 | 0.1771 | 0.1379 | 0.0577 | 0.0294 | 0.0498 | |||
| p=0.3 | 0.3606 | 0.1623 | 0.2941 | 0.1920 | 0.0937 | 0.1626 | 0.0373 | 0.0200 | 0.0329 |
a
The χ2 factors in the table are calculated using equations 1–3 in the online data supplement. Multiply by N (the number of cases) to calculate the desired χ2 value. α=proportion of misclassified controls in the sample; p=proportion with genetic marker in case sample; q=proportion with genetic marker in control sample; t=ratio of controls to cases.
Examples Illustrating How to Use Table 1
Example 1.
Consider a sample with equal numbers of cases and controls (120 of each), and we will see what happens when 10% of the controls sample have the disease (i.e., α=0.1). Say that the true prevalence of the marker is 20% in cases, as opposed to 10% in unaffected individuals (i.e., p=0.2, q=0.1). The upper half of Table 1 shows results for α=0.1, and the first part of that section shows results for equal numbers of cases and controls (t=1). Look in the cells corresponding to p=0.2, q=0.1. The first cell gives the factor for χ2CC, which is 0.0392. To apply that factor to our data set, multiply it by the number of cases (0.0392×120), which reveals that the chi-square test statistic for an ideal sample of that size, with no misclassified controls, would be about 4.70—statistically significant at the 5% level. Now imagine that 10% of the 120 controls (i.e., 12 controls) are misclassified and actually have the disease. The next cell in the results for p=0.2 and q=0.10 gives the factor for χ2MC, which is 0.0309. Multiplying this factor by 120 yields 3.71—no longer significant. Finally, if we remove the 12 misclassified controls from the sample, we use the third cell in that box, a factor of 0.0366, yielding χ2reduced=120×0.0366=4.39—again significant, even though the sample is now smaller.
Example 2.
Consider a sample with twice as many controls as cases (100 cases, 200 controls), and see what happens when 25% of the controls in the sample have the disease (α=0.25). Use the same p=0.2 and q=0.1 as in the first example. We look to the lower half of the table for α=0.25, the lower section of which shows results for samples with twice as many controls as cases (t=2). Again find the results for p=0.2 and q=0.10, and see that the factor for χ2CC is 0.0577. To determine the value of χ2CC, multiply this factor by the number of cases (not the number of controls), which yields χ2CC=100×0.0577=5.77 (significant). Following the same steps as in example 1, we see that χ2MC=100×0.0294=2.94 (not significant) and χ2reduced=100×0.0498=4.98 (significant). This example also illustrates how a proportion of 25% misclassified controls has a much more serious effect than one of 10%.
These two examples illustrate how to use Table 1. Readers who wish to calculate the chi-square factors for values of p, q, α, and t other than those listed in the table can refer to part 1 of the data supplement that accompanies the online edition of this article.
Patterns and Rule of Thumb
The numerical results in Table 1 reveal two interesting patterns. First, the greater the difference between the proportions of the genetic marker in cases and controls, the easier the association is to detect, as expected. We see this by comparing χ2 values between different p-q combinations, which reveals that the greater the difference between p and q, the greater the χ2 factor. For example, in any one of the subsections of the table, the χ2 factors are greatest when p=0.30 and q=0.05. Second, the information lost by removing the misclassified controls, represented by χ2reduced, is far less than that lost by leaving them in the control sample. We see this by comparing the three χ2 values within each p-q combination. Consistently, χ2MC (misclassified) is markedly less than χ2CC (correctly classified), whereas χ2reduced is only slightly less than χ2CC.
Theoretical calculations (see part 2 of the online data supplement) reveal that the ratio of χ2MC to χ2CC, which we can call the “including misclassified controls ratio,” is around (1–α)2. Thus, if 10% of controls are misclassified, the χ2 drops to about (0.9)2, or 81%, of the value it would have had if all controls had been correctly classified, and if 25% are misclassified, it drops to about (0.75)2, or 56%. In contrast, the ratio of χ2reduced to χ2CC, which we can call the “removing misclassified controls ratio,” is only about 1–α. If 10% of controls are misclassified, this ratio is 90%, and if 25% are misclassified, it is 75%.
These results lead to a simple rule of thumb: If the proportion of misclassified controls in the sample is α, then the study's informativeness will be reduced to about (1–α)2 if the misclassified controls are left in the study, but only to about 1–α if they are removed.
Table S2 in the online data supplement lists values of these two ratios for the same setups examined above in Table 1 and shows that the actual ratios are reasonably close to those from the rule of thumb.
When Increasing the Number of Controls Does Not Improve Power
Whether or not one's sample contains misclassified controls, it can happen that the sample is not large enough to achieve statistical significance. In that situation, one can try to increase the sample size, so as to improve statistical power. Unfortunately, if one has a limited number of cases and can collect only more controls, there is an upper limit on statistical power (4). We illustrate this fact by showing the maximum value that χ2 can achieve in the following example.
Example 3.
Imagine you are conducting a study in which the true prevalence of the genetic marker is 10% in cases and 5% in controls (thus, p=0.10, q=0.05), and say your initial sample contains 50 cases and 50 controls (N=50, t=1). You can collect more controls if needed, but not more cases. Assume in this example that all controls are correctly classified. Table 1 yields a χ2 factor of 0.0180. Multiplying by N yields 0.0180×50=0.90 for the approximate χ2—nowhere near sufficient for statistical significance. Intuitively, you might think that if you could collect enough additional controls, you could raise that χ2 factor to an acceptable value, but that is not the case. In this example, the χ2 cannot be made larger than 2.63, no matter how many controls you collect. 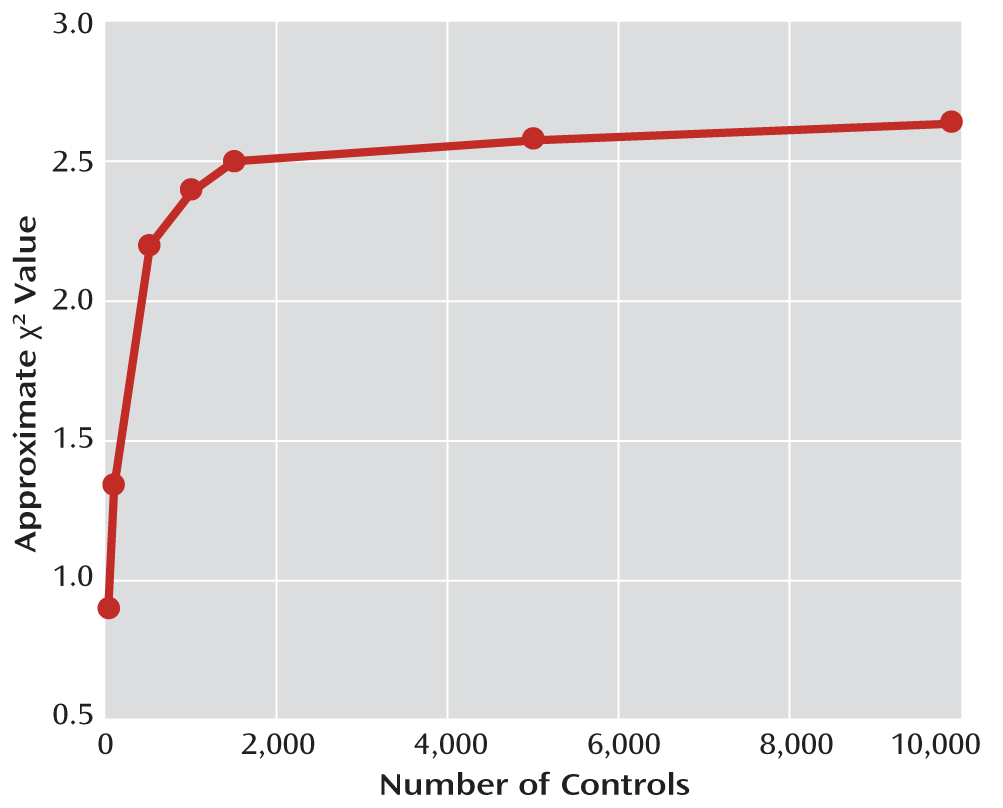Figure 1 illustrates this: If you increase the number of controls from 50 to 100, the χ2 rises from 0.90 to 1.34, which is a nice improvement. However, even using 1,000 controls will only raise the χ2 to 2.40, and after 2,000 controls, the curve practically levels off, slowly approaching its maximum value of 2.63.
FIGURE 1. One Example of a Chi-Square Value as a Function of an Increasing Number of Controls, in a Perfect Sample With 50 Casesa
a In this example, p=0.10 and q=0.05—that is, there is a true association, with the genetic marker occurring in 10% of cases and 5% of controls. There are no misclassified controls in this example. The graph shows how the χ2 value approaches its maximum possible value of 2.63 as the number of controls increases. Increasing the number of controls to 10–20 times the number of cases will raise the χ2 value to about 80%–90% of the maximum value, but beyond that, increasing the number of controls has little effect.
To calculate the maximum possible χ2 value for other numbers of cases and other values of p and q, see equation 4 in the online data supplement.
Discussion
Summary
We have shown that if 10% of the controls in a sample are misclassified, that is, are actually affected with the disease under study, the sample's informativeness falls to about 75%–80% of what it would have been if all controls had been correctly classified; and if 25% of controls are misclassified, informativeness falls to around 50%, where we measure informativeness via the chi-square value from a “perfect” sample. These results are robust and do not depend on the true proportions of the genetic marker in the cases and controls or on whether there are equal numbers of cases and controls. Removing the ill controls from the control sample restores much of that lost informativeness and more than compensates for the reduced sample size. In this sense, the misclassified controls are “worse than useless” for analysis.
We have illustrated the effects when α is as high as 10% or 25%. If α is very low, the effect of misclassification is minor. For example, if α is only 1%, then (1–α)2 is 98%, and 1–α is 99%; the study's informativeness is hardly reduced at all, whether the misclassified controls are left in or not. Thus, these issues may be of less concern for rare psychiatric conditions such as schizophrenia.
Readers should bear in mind that these chi-square values do not measure statistical power directly. A user who wants to estimate power should use appropriate power formulas (see reference 3, for example) or run computer simulations to do so.
Additionally, we have illustrated how if one has a limited number of cases available, then once past a certain point, increasing the number of controls no longer adds statistical power to one's study. This fact is well known in biostatistics (see reference 4, for example) but has not been widely recognized in psychiatric genetics. One implication is that consortia or repositories with very large numbers of controls may be of limited usefulness for some studies.
Issues
The reader may ask, “If I can identify which of my controls are misclassified, couldn't I simply move them into the 'cases' category—wouldn't that be better than removing them from the study altogether?” Yes, in the ideal situation in which one may be certain that the misclassified controls actually meet one's diagnostic criteria for the disease of interest, counting them as cases will increase statistical power. However, if there is uncertainty about their diagnoses, it is better simply to remove them from the study (5). Our results show that the loss in informativeness from doing so is not as severe as leaving them in as controls would be.
Ongoing discussions in psychiatric genetics concern just how damaging misclassified controls may be to a case-control study. Some have argued that it is all right to have misclassified controls in one's sample as long as one collects a sufficiently large sample to “counteract” their effect (see reference 6, for example). However, we have also illustrated how simply collecting more and more controls does not necessarily solve the problem, since beyond a certain point, additional controls add no more statistical power. Schwartz and Susser (7, 8) have argued that using “well” (i.e., screened) controls actually undermines validity. However, their argument addresses the situation in which investigators use stricter criteria for the controls than for the cases, such that cases and controls are no longer comparable. They do not address the more general situation in which comparable criteria are used for both groups, which is our concern here.
Footnote
Received Nov. 14, 2011; revisions received Jan. 30 and March 15, 2012; accepted March 15, 2012.
Supplementary Material
Supplementary material
- View/Download
- 101.74 KB
References
1.
Tsuang MT, Fleming JA, Kendler KS, Gruenberg AS: Selection of controls for family studies: biases and implications. Arch Gen Psychiatry 1988; 45:1006–1008
2.
Wickramaratne PJ: Selecting control groups for studies of familial aggregation of disease. J Clin Epidemiol 1995; 48:1019–1029
3.
Moskvina V, Holmans P, Schmidt KM, Craddock N: Design of case-control studies with unscreened controls. Ann Hum Genet 2005; 69:566–576
4.
Fleiss JL, Levin B, Paik MC: Statistical Methods for Rates and Proportions, 3rd ed. Hoboken, NJ, Wiley-Interscience, 2003
5.
Greenberg DA: There is more than one way to collect data for linkage analysis: what a study of epilepsy can tell us about linkage strategy for psychiatric disease. Arch Gen Psychiatry 1992; 49:745–750
6.
Wellcome Trust Case Control Consortium: Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature 2007; 447:661–678
7.
Schwartz S, Susser E: Genome-wide association studies: does only size matter? Am J Psychiatry 2010; 167:741–744
8.
Schwartz S, Susser E: The use of well controls: an unhealthy practice in psychiatric research. Psychol Med (Epub ahead of print, Sept 1, 2010)
Information & Authors
Information
Published In
History
Received: 14 November 2011
Revision received: 30 January 2012
Revision received: 15 March 2012
Accepted: 15 March 2012
Published online: 1 August 2012
Published in print: August 2012
Authors
Funding Information
Dr. Weissman has received research support from NIMH, the National Institute on Drug Abuse, NARSAD, the Sackler Foundation, the Templeton Foundation, and the Interstitial Cystitis Association and receives royalties from Perseus Books, American Psychiatric Press, Oxford University Press, and Multi-Health Systems. The other authors report no financial relationships with commercial interests.Supported by NIMH grants MH60912 (to Dr. Weissman), MH37592 (to Dr. Donald F. Klein and Dr. Fyer), MH65213 (to Drs. Subaran and Hodge), MH48858 (to Dr. Hodge), and MH090966 (to Drs. Jay Gingrich, Weissman, and Hodge).
Metrics & Citations
Metrics
Citations
Export Citations
If you have the appropriate software installed, you can download article citation data to the citation manager of your choice. Simply select your manager software from the list below and click Download.
For more information or tips please see 'Downloading to a citation manager' in the Help menu.
View Options
View options
PDF/EPUB
View PDF/EPUBLogin options
Already a subscriber? Access your subscription through your login credentials or your institution for full access to this article.
Personal login Institutional Login Open Athens loginNot a subscriber?
PsychiatryOnline subscription options offer access to the DSM-5-TR® library, books, journals, CME, and patient resources. This all-in-one virtual library provides psychiatrists and mental health professionals with key resources for diagnosis, treatment, research, and professional development.
Need more help? PsychiatryOnline Customer Service may be reached by emailing [email protected] or by calling 800-368-5777 (in the U.S.) or 703-907-7322 (outside the U.S.).