While there is growing acknowledgment of the importance of moderators and mediators in medical research, it is not clear that clinicians appreciate the impact of these issues, nor that clinical researchers clearly address and communicate these issues to clinicians.
In part, this situation reflects the history of the development of these topics. The terms appear to have originated in social psychology, and they were long used without specific definitions. In 1986, Baron and Kenny (
1) proposed clear conceptual definitions that changed the picture. In general, moderators and mediators describe two types of three-factor associations. In a randomized clinical trial specifically, a moderator of the effect of treatment choice (treatment versus control) on outcome suggests
on whom or
under what conditions treatment choice differentially affects outcome. Moderators are the basis of personalized medicine (
2–
4) suggesting how best to match treatments to individual patient needs. A mediator of treatment outcome suggests
how or
why the treatment condition might be preferred to the control condition in the population sampled (
5–
7), suggesting how treatment outcome might be improved.
Baron and Kenney (
1) also proposed an analytic approach based on linear models to document moderation or mediation. For application in clinical research, what was originally proposed was not completely satisfactory, for it did not clearly distinguish moderation from mediation (
5). Applications often identified factors as moderator-mediators and mediator-moderators, perpetuating confusion. In any case, the linear model used was based on assumptions that sometimes do not accurately reflect reality and can mislead clinical decision making. Around 2000, the MacArthur model was proposed (
5,
7,
8), which clarified the distinction between moderation and mediation for clinical research (risk research and randomized clinical trials), indicated how and when linear models might be used to document these associations, and opened the door for further methodological development. However, one consequence of this long and somewhat scattered history is that moderators/mediators of treatment outcome in clinical trials are still often ignored or incorrectly handled, and the messages to clinicians resulting from such trials are consequently either unclear or simply wrong.
In what follows, I review and integrate the current knowledge of these topics so that clinicians and clinical researchers might better appreciate them. The emphasis is on population inferences—on what might be learned from trial reports that apply to a clinician’s own patients. (For a brief discussion of the statistical methods researchers need to apply these principles, see the data supplement that accompanies the online edition of this article.)
I will begin by proposing an effect size comparing treatment and control conditions that can be used to assess the clinical significance of the choice between them, whatever the outcome measure, and whatever the population, necessary to these considerations. This is a necessary precursor to understanding moderators and mediators, which are in essence dissections of the effect size.
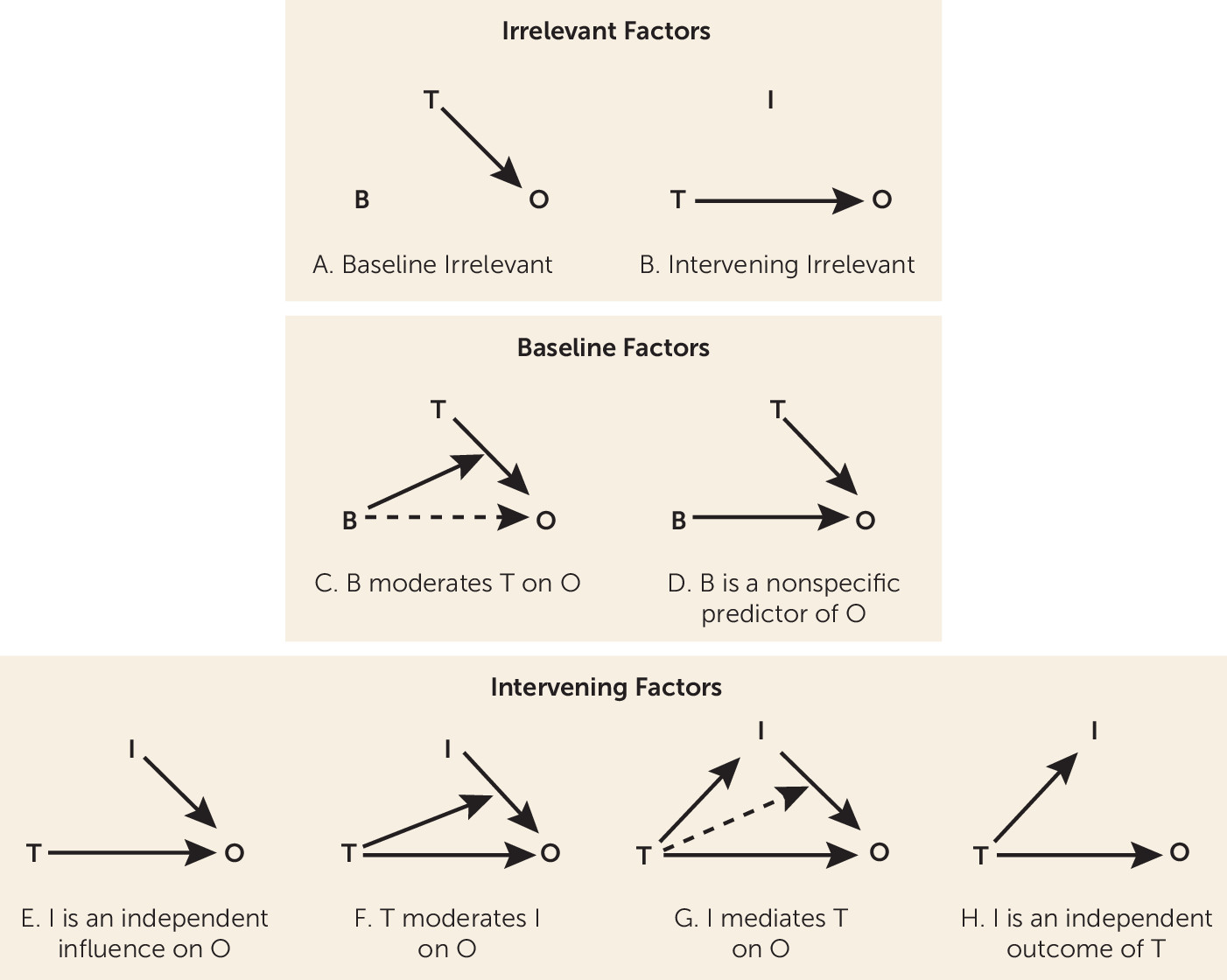
The factors (often called “covariates”) to be discussed are of two types: baseline (pre-randomization) factors and intervening factors—events or changes that occur during the trial before outcome is determined. Next, I address the irrelevant factors (either baseline or intervening)—factors that researchers should ignore in evaluating trial results and that clinicians should ignore in making decisions between a study’s treatment and control conditions. A factor that is not irrelevant is termed a predictor. Next, a section is devoted to the roles that a baseline predictor may play: as a moderator or as a nonspecific predictor. Another section covers the various roles that an intervening predictor may play: as a mediator, as an influence on the outcome independent of treatment choice, as a consequence of treatment independent of the outcome, or as a predictor moderated by the effect of treatment choice on the outcome.
These exhaust the possibilities of how baseline and intervening factors can be related to treatment choice (
Figure 1), and they clarify why the focus both for clinical research and clinical decision making should be
only on moderators and mediators of treatment outcome. More important, the discussion identifies many errors that are common in randomized controlled trials in dealing with baseline and intervening factors, to guide clinicians as to which trials might be ignored and which considered carefully, and to persuade clinical researchers away from study designs and analyses that clinicians might best ignore.
Effect Sizes and p Values
Because moderators/mediators reflect dissection of the influences on the causal effect of treatment, it is necessary to appreciate the distinction between significance levels, p values, and effect sizes. Unfortunately common in clinical research is misinterpretation of and an overemphasis on p values, so much so that many have suggested banning the p value entirely (
9,
10). The significance level of a statistical test, usually denoted by
alpha, is a general declaration of how tolerant a field is for false positive results. By consensus, the significance level is usually set at 5%. In contrast, the p value is a statistic computed from study data to be compared with alpha: A result is declared “statistically significant at the alpha level” if the p value is less than alpha. The primary influence on the p value is sample size, but the p value is also affected by the choice of measures and design and analytic procedures—in fact, by any design decision related to considerations of statistical power (
11,
12)—and only incidentally by the effect size, an indication of the clinical significance of the finding.
To ethically propose a randomized trial comparing treatment and control conditions, there must be a theoretical rationale and empirical justification for the hypothesis that the two conditions differ (
13). In such a trial, there is little to no chance of
absolute equality of treatment effects on outcome (
14,
15), but the outcome difference may certainly be trivial and of no clinical importance. However small the nonnull effect between treatment and control conditions, there is always a sample size large enough to result in a p value as small as desired. That is what power considerations in designing a trial address (
11).
For that reason, a statistically significant result means only that the sample size was adequate to detect some deviation from the null hypothesis that the treatment and control conditions are absolutely equivalent. It does not mean that the deviation was of any clinical significance. Conversely, a statistically nonsignificant result means that the sample size was not adequate to detect any deviation from the null hypothesis, as a result of some flaw in the rationale, design, or execution of the study. The treatment difference may in fact be clinically significant, but it would require a better-designed trial, or combination with other valid trials in a meta-analysis, to demonstrate that fact. Clinicians would be well advised to ignore nonsignificant findings in the research literature as inconclusive, and with statistically significant findings, to focus on effect sizes, not p values.
To assess clinical significance, every p value (significant or not) should be accompanied by an effect size that indicates clinical significance and a confidence interval that indicates estimation precision (
16). The 95% confidence interval of a statistically significant effect size (at the 5% level) will not include the null value indicating absolute equivalence of the two treatments; that of a statistically nonsignificant effect size will. A clear distinction between a statistically significant effect (p<0.05) and a clinically significant one is crucial.
For a trial comparing treatment and control conditions, there are many possible forms of effect sizes, depending on the nature of the outcome measure (
17–
20). For clear interpretation by clinicians, however, the
success rate difference (SRD) (
20) is recommended: this is an effect size that can be estimated regardless of the nature of the outcome measure(s) (see the online
data supplement). If one were to randomly select one patient from the population who was assigned to the study treatment and another who was assigned to the control condition, what is the probability that the study-treatment patient has an outcome preferable to that of the control patient, less the probability of the opposite? Answer: SRD (
20,
21).
An SRD of 0 indicates no overall differential effect of study treatment versus control condition in the population sampled (i.e., consistent with, but not the same as, absolute equivalence of the two). The SRD ranges from −1 to +1. An SRD >0 indicates that, overall, the study treatment condition is preferred to the control condition. The SRD comparing study treatment versus control condition is the negative of the SRD comparing control condition versus treatment. For the purposes of this discussion, it is assumed that the treatment condition is overall preferred (however trivial that preference). An SRD of +1 means that every patient given the study treatment has an outcome preferable to that of every patient in the control condition.
Number needed to treat (NNT) equals 1/SRD. If one were to sample random pairs of patients and give one the study treatment and assign the other to the control condition, and declare each patient a “success” if his or her outcome was clinically preferable to that of the paired partner, how many pairs would one have to sample to expect to find one more success among the study treatment patients than among the control patients? Answer: NNT (
22–
27). It makes a major difference both to patients’ well-being and to medical costs whether the NNT=2, 20, or 200, because the larger the NNT, the more patients are given the study treatment unnecessarily; they would have done just as well in the control condition.
Cohen’s standards for effect sizes in trials comparing two treatments for acute conditions (
12) suggest that a “small” effect would be an SRD of 0.11 (NNT=9), a “medium” effect would be an SRD of 0.28 (NNT=4), and a “large” effect would be an SRD of 0.43 (NNT=2). These are reasonable experience-based signposts. However, in specific situations, these standards might be quite different. For example, the NNT for the Salk polio vaccine was about 2,500: that is, 2,500 children needed to be vaccinated to prevent one case of polio. Generally, the assessment of how large an SRD (how small an NNT) is convincing evidence for choosing one treatment rather than another depends on the nature of the disorder being treated, the consequences of unsuccessful treatment, the costs and risks associated with treatment, and so on, and it is ultimately the decision of the individual clinician or patient.
However, in designing a trial, researchers must declare
their threshold value for a clinically significant effect size. An adequately powered trial is one with at least, say, an 80% chance of detecting any effect size larger than that threshold (
11). Unfortunately, researchers often set that threshold (SRD) much higher than they would as clinicians for their own patients, just to keep the necessary sample size small. Too small a sample size is the major reason for statistically nonsignificant findings.
The overall effect size comparing study treatment versus control condition in a population sampled is important, for if the decision were to use only one treatment for all in the population, it indicates how much better off the population would be if the study treatment were chosen rather than the control condition. However, within that population, some individual patients may benefit more than others from the study treatment, and some may even be harmed by a study treatment that has overall benefit. That observation motivates the search for sources of variation in the effect size among patients within the population, and brings us to the issue of moderators and mediators.
Linear models continue to be the most common statistical approach to documenting moderators or mediators. The advantage of linear models is that they facilitate easy computations—statisticians love them! The concomitant cost, however, is that they are based on assumptions that often do not hold. To avoid such assumptions (as well as to simplify the math), we will focus on categorical factors, two or more ordered or nonordered categories. If the baseline/intervening factor of interest is continuous, it might be grouped—for example, age may be grouped by decade: ages 20–29, 30–39, and so on. Moreover, each category may be based on multiple individual factors—for example, combinations of gender, age, baseline illness severity, and biomarkers. This approach allows consideration of the various roles factors may play in identification of individual differences among patients in response to study treatment versus control condition without imposing any restrictive assumptions. (This does not preclude the possibility of using linear or other models to apply these principles. See the online data supplement.)
The population sampled in a trial can be organized as shown in
Table 1, with the predictors presented in M categories, labeled 1,2,3,…, M defining the rows, Treatment and Control (T1 and T2) the columns. The probabilities that patients randomized to the study treatment and to the control condition (whatever the proportion assigned to each) fall into each cell are coded as P
i±D
i. Then P
i is the average of the probabilities that individuals in the treatment or control group assigned to the i-th category, and D
i the half-difference between those two probabilities. In a trial sample, these probabilities are estimated by the proportions of those in each treatment group found in each cell.
The overall effect size, SRD, compares the outcomes between every study treatment patient versus every control patient, ignoring the categories. There are also separate SRDs comparing patients in category i assigned to the study treatment with patients in category j assigned to control condition: SRD(i,j) (M2 of these). Of special interest are the effect sizes within each category: SRD(i,i) (M of these), and SRDW is the average of the SRD(i,i). These are the necessary basic tools.
Irrelevant Factors
A crucial starting point: If SRD(i,j)=SRD for all pairs of categories, then the factor that defines the categories is
irrelevant to treatment outcome (
Figure 1A,B) and should be ignored by clinicians in deciding between these treatments, as well as by clinical researchers in studies evaluating these treatments.
The problem is that, in the absence of the knowledge that certain factors are irrelevant, clinical researchers often propose to use them either to match or block patients in sampling or to “adjust” for those factors in the analysis of trial outcomes. At best, to do so costs power in testing and precision in estimation, but at worst, it may introduce error into the conclusions (
28). In short, inclusion of irrelevant factors in analysis of trials confuses the issue of choosing between the study treatment and the control condition.
If a baseline or intervening factor is not irrelevant, it is a predictor. The remainder of this discussion will focus only on predictors. Note, however, that researchers often use the term “predictor” loosely to include all baseline and intervening factors, including irrelevant factors, and some use that term even more loosely for factors that do not even temporally precede the outcome.
Baseline (Pre-Randomization) Predictors
With randomization, all baseline predictors (at the population level) are independent of treatment choice (Di=0 for all i). In any trial, the sample estimates of all Di are unlikely to be zero, but in replications, the mean value over replications (the population value) of each Di will be zero.
Key here is the understanding that randomization in a trial does not result in two matched samples assigned to study treatment and control condition; it results in two random samples from the same population. Thus, in a trial, each baseline factor has a 5% chance of a statistically significant difference between the two treatment groups. Too close a match between those randomized to the two treatment groups should raise questions about the randomization procedure, as would too poor a match.
Nevertheless, what often happens is that, after noting baseline factors that significantly differentiate the two samples in a trial, the researchers propose to “adjust” for those factors in analysis. This is “post hoc” hypothesis testing. In each replication, different baseline factors will be found “statistically significant,” and since the research question shifts depending on which factors are used to “adjust” and how “adjustment” is done (
28), the conclusions will also change. This creates the unfortunate impression of nonreplicability of research results, and it confuses clinical decision making.
A baseline predictor is a
moderator of the effect of treatment choice on outcome if SRD(i,i) is not the same for all categories, that is, if the effect of treatment changes depending on which category patients belong to (
Figure 1C). For example, the study treatment may be better than the control condition for males, but the reverse may be true for females, in which case gender moderates the treatment effect. In general, it may be that SRD(i,i) is large and positive for some categories, large and negative for others, and trivial in magnitude for the remaining. Then clinicians should choose the study treatment over the control condition for the first groups, the control condition over the study treatment for the second, and choose whichever is more convenient or less costly for the remaining.
Generally, if the overall effect size (SRD) is large, that will reflect the effect size for the majority of patients in the population, but not necessarily all. However, the overall effect size (SRD) may be zero if half the population are in categories with SRD(i,i) much greater than zero and the other half in categories with SRD(i,i) equally much less than zero (
29). Interpreting a large magnitude of SRD as indicating the general superiority of one treatment over the other is correct, but interpreting a near-zero magnitude of SRD as showing equivalence of the two treatments may be a very serious mistake, for there may be different treatment effects
within the population. Ignored moderators may be one explanation for why so many psychiatric treatments appear to have such low effectiveness.
The clinical importance of a moderator can be estimated by comparing the preferred treatment versus the nonpreferred for each patient. That would switch all negative SRD(i,i) to positive, and would generally increase the SRD. Comparing the SRD of the preferred versus the nonpreferred treatments with the SRD of study treatment versus control condition indicates the clinical importance of a moderator (
30).
On the other hand, when SRD(i,i)=SRD
W for all i, the baseline predictor is a
nonspecific predictor of treatment outcome (
Figure 1D). Now, regardless of the category, the same treatment is equally preferred for all. Hence, nonspecific predictors are of no use in making decisions between the two treatments.
Unfortunately, the predictors used for “adjusting” in trial designs are often assumed to be nonspecific predictors, even when they may be moderators (e.g., in using analysis of covariance). Researchers do this to shift the focus to an SRD
W wrongly assumed to equal SRD(i,i) for all i, and away from the usually smaller overall SRD, thus decreasing the sample size necessary to achieve statistical significance. However, if such a baseline factor is a moderator and not a nonspecific predictor, the conclusion based on such an analysis will be wrong. How wrong depends on the impact of the moderator. Consequently, in reading the report of a randomized controlled trial in which such matching, blocking, or “adjusting” is done, a clinician should check that the researchers’ “a priori” evidence that the factors used were predictors, and indeed nonspecific predictors and not moderators, for if that evidence is absent or wrong, the conclusions are questionable. Moreover, proposal reviewers should have checked the documentation for the relevance of such factors before the trial begins, and the trial registration at
ClinicalTrials.gov should specify those factors.
Just as many researchers include irrelevant factors in the term “predictors,” many researchers use the term “confounders” to include all baseline factors, irrelevant or predictor. The technical definition of the term “confounder” (
31) in a randomized controlled trial requires that the factor be correlated with both treatment choice and outcome in the population. Since in a randomized controlled trial no baseline factor is correlated with treatment choice, no baseline factor can be a confounder. Nevertheless, many researchers focus a great deal of unwarranted attention on such “confounders.” To be fair to researchers, reviewers of proposals and journal submissions often demand such attention.
Intervening Predictors
Consider an intervening predictor. Now randomization does not guarantee independence. Either treatment choice is not correlated with that factor (i.e., all the D
i’s in
Table 1 are zero) or it is (i.e., some of the D
i’s in
Table 1 are nonzero).
Consider the first situation (all the D
i’s equal zero). Then either the intervening factor is an
independent influence on the outcome (independent of the treatment,
Figure 1E), or
treatment choice moderates the effect of the intervening factor on the outcome (
Figure 1F). Note the reverse direction of moderation here.
To see the distinction between these two, consider the example of a trial comparing a study treatment (a new drug) versus a control condition (placebo) for major depressive disorder, where the outcome measure is a decrease in symptoms over a 1-year period. An intervening predictor might be whether or not a death in the patient’s family occurs during that year. Clearly such an event may affect symptom severity, but treatment choice is unlikely to change the probability of such a death. If the association of that event with outcome is the same in both treatment groups, thus having no differential impact on outcome, then that event is an independent influence on outcome (i.e., independent of treatment choice).
However, it may be that the study treatment here increases patients’ ability to cope with such events better than does the control condition. Then the effect of the death on outcome may be stronger in one treatment group than in the other, and treatment choice moderates the effect of that event on outcome (not vice versa). In either of these cases, the intervening factor does not play any role in deciding between the two treatments.
On the other hand, if the intervening factor is correlated with treatment choice (some D
i≠0, e.g., change in coping ability in the above example), that would suggest that such a change may be part of the process by which treatment choice affects outcome. Then the issue is how much of the treatment versus control effect on outcome is transmitted via the intervening factor. This can be estimated by setting all the D
i to zero and computing SRD in the absence of any correlation (the
direct effect). The difference between the overall SRD and the direct effect (the
indirect effect) indicates the impact of mediation (
17). If the indirect effect is nonzero, then the intervening factor is a
mediator of treatment outcome (
Figure 1G). (All mediators are “confounders,” but not all “confounders” are mediators.)
Examination of the various SRD(i,j) might then suggest manipulations of treatment protocol for the preferred treatment that might improve its effectiveness or cost-effectiveness relative to the nonpreferred. For example, if in the above example it were found that the study treatment increased coping ability more than did the control condition, and that this explained part or all of the advantage of the study treatment over the control condition, then it is the change in coping ability (not the death in the family) that mediates the effect of treatment choice on outcome. Then adding components to the study treatment protocol that would further improve coping ability (perhaps adding psychotherapy to drug) might increase that overall SRD.
If the intervening factor is correlated with treatment choice but is not a mediator, then the intervening factor is an
independent outcome of treatment choice (
Figure 1H). For example, if the study treatment were a diet intervention intended to produce weight loss (compared with treatment as usual as the control condition), the study treatment might also result in a greater early increase in self-confidence than the control condition. If that change explained no part of the treatment difference in the intended outcome (weight loss), change in self-confidence would be an independent outcome of the treatment-versus-control choice, which is, of course, interesting but does not affect the choice between the two for weight loss. On the other hand, if that change in self-confidence did explain some part of the treatment-versus-control difference in weight loss, then change in self-confidence would be a mediator of treatment outcome, and incorporating components into the study treatment that might further increase self-confidence might be considered in hopes of further increasing the differential effect on weight loss.
Discussion
The terms above are summarized in the schematics of
Figure 1, where B is a baseline factor, I an intervening factor, T the choice between Treatment and Control, and O the outcome measure. What is crucial is that the only times a factor affects the treatment choice to improve O in the population sampled are when B is a moderator or I is a mediator of treatment outcome. Irrelevant factors are of no use at all. Other predictors may be of clinical interest but for reasons having nothing to do with deciding between the two treatments.
All things considered, clinicians should ideally look first to large, simple, preferably multisite randomized clinical trials (
32,
33) and subsequent exploration of the resulting data set to guide the choice of a new treatment over a control condition. That would mean:
•
Populations sampled that well represent the full range of patients for whom clinicians might have to make that decision. Exclusions on the basis of moderators (e.g., baseline comorbidities) limit generalizability of the conclusions.
•
Simple randomization to treatment and control conditions (no matching or blocking) at each site.
•
A control/comparison group that represents what clinicians are currently using (usually not placebo or nocebo).
•
Outcome measures that best represent the clinical benefit-to-harm balance in individual patients (
34,
35) that would be used to compare outcomes between patients.
•
Adequate statistical power (say 80%) in a single-site trial to detect any clinically significant effect size. What researchers set as their threshold of clinical significance should be explicitly stated and justified. In a multisite study, there should be adequate power to detect any clinically significant SRDW. In a multisite study where site does not moderate treatment effect, SRDW is the effect size at each site. In a multisite study where site does moderate treatment effect, SRDW is the typical (average) effect size over all sites represented by those in the trial.
•
In analysis, no “adjusting.” In a multisite study, site differences and site-by-treatment interaction must be included in every analysis (
36).
•
A report of SRD and its confidence interval in a single-site study. In a multisite trial, the SRD at each site and its confidence interval, the SRDW and its confidence interval, and baseline descriptive statistics for each site should be presented. If there are site differences in the site-specific SRDs, these might allow clinicians to identify sites most like their own to help guide their decision making.
In designing such trials, clinical researchers should carefully consider the rationale and justification for baseline factors that might be moderators and intervening factors that might be mediators, and measure each such factor as reliably and validly as possible, avoiding multicollinearity and missing data. However, these factors should not affect the primary analysis; these are the materials for follow-up exploratory studies. Clinicians should be encouraged to seek out such exploratory studies to further refine their thinking about clinical decision making between treatment and control conditions, and clinical researchers for rationale and justification for subsequent randomized clinical trials.
Once moderators are detected, research might focus first on confirming the moderators found in exploration (see the online data supplement), and, if confirmed, subsequently on new randomized controlled trials on the moderator-defined subpopulations and the exploration for possible mediators in the total population (in absence of moderators) or in the separate subpopulations (defined by moderators) in which the study treatment is preferred to the control condition and the control condition is preferred to the study treatment. If mediators are detected, confirmatory randomized controlled trials might then follow (see the data supplement).
This is not the way randomized clinical trials are currently done. Many trials use very stringent inclusion and exclusion criteria, sometimes excluding the majority of the population clinicians are required to treat (
37). Many trials are single-site, and when the same treatment comparison is done in trials at other sites, the results do not replicate (
38). This problem arises because different single-site trials often use different designs and analyses, which makes it impossible to assess how much of the nonreplication is due to methodological differences, how much to true site differences in effect sizes, and how much to the fact that some conclusions are simply wrong. In many cases, trials are underpowered (
39). The value of multisite trials is that all sites follow the same protocol, that differences of the site SRDs reflect true differences among the sites, and that they are more likely to be adequately powered. However, many multisite trials assume absence of site differences in SRD (no site-by-treatment interaction), in which case their conclusions too may be wrong (
36). Many trials use placebo, nocebo, or other control/comparison treatments not usually used in clinical practice, which is unlikely to convince clinicians to change what they are doing. Many of the statistically nonsignificant treatment effects are erroneously interpreted as indicating equivalence of the two treatments. Many statistically significant but clinically trivial treatment effects are presented as important only because p is less than 0.01 or 0.001. Many trials use outcome measures of little interest to clinicians and patients (in Tukey’s terms [
40], “good” measures, not the “right” ones), and many report multiple outcome measures separately, where the best choice of treatment differs from one measure to another, rather than one evaluation of the benefit-to-harm balance for individual patients. Many trials conduct subgroup analyses rather than moderator analyses (
41,
42), that is, stratifying the population on some baseline factors and reporting p values comparing the two treatments separately in each stratum, rather than comparing the effect sizes from the various strata with each other. Many trials match, block, or “adjust for” baseline factors, some collinear, some irrelevant, some incorrectly assumed to be nonspecific predictors, often mixing irrelevant factors with both baseline and intervening predictors that play quite different roles with respect to the decision between the study treatment and the control condition.
Clinical researchers often complain that the results of their research are very slow to have an impact on clinical decision making. However, given the problems cited above, that should be no surprise. At the same time, clinicians and patients who want clinical decision making to be evidence-based are left with the problem of identifying which of the clinical research reports should be ignored (
38,
43) and which carefully considered.
Why has this happened? First, there is a common but mistaken belief that 1) the more covariates are used in “adjustment,” the more correct the answer, 2) inclusion of too many covariates can do no harm, and 3) the assumptions of linear models do not really matter. The arguments presented here are meant to question those beliefs. Then too, clinical researchers often seem to use complex models, hoping that by eliminating “distractions,” they might find a simple answer. However, the true answer is often not simple, and the “distractions” may contain the truth. The treatment-versus-control effect may not be the same for all in the population (moderators), or work the same in different subpopulations (mediators). There are irrelevant factors, and predictors that do not have an impact on the decision between the study treatment and the control condition. Efforts to remove these as distractions or mixing them up can compromise a true answer. In short, a better approach is via simple methods in multiple stages, ultimately leading to complex but true answers. Such simple approaches are often discouraged, labeled as “lacking sophistication.” Much of this situation is related to lack of understanding of the issues of moderation and mediation of treatment outcome in randomized controlled trials, and why and how this affects both trial design and analysis, and, more important, clinical decision making.