A Continuous Clustering Algorithm for Detection of Local Sleep in Humans
Abstract
Objective:
Methods:
Results:
Conclusions:
Methods
Computation of the Instantaneous Amplitude and Frequency
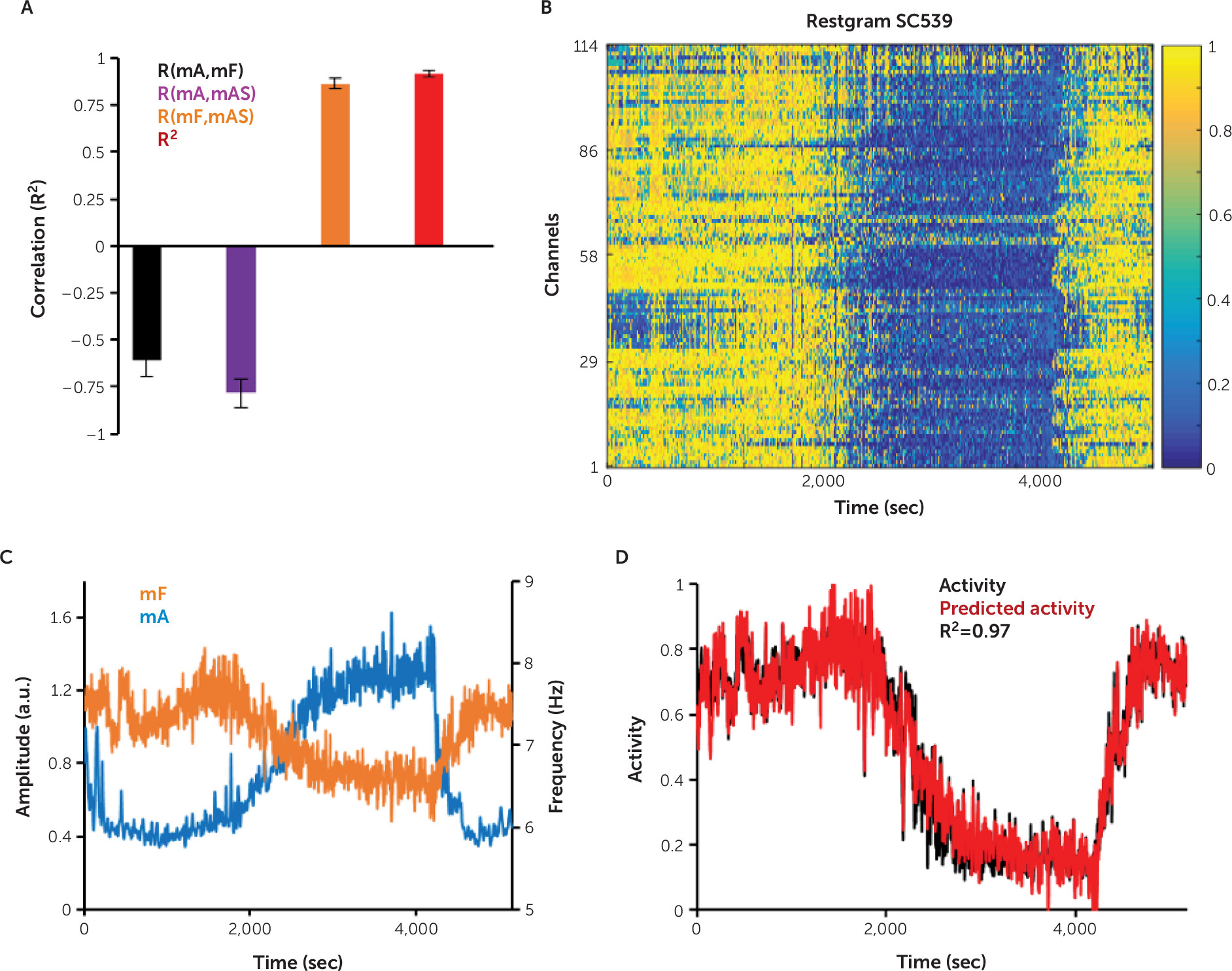
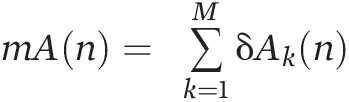 , where δAk is the amplitude of channel k, M is the number of channels, and n is the time moment. We denoted as mF the average over all channels of the frequency θαF,
, where δAk is the amplitude of channel k, M is the number of channels, and n is the time moment. We denoted as mF the average over all channels of the frequency θαF, 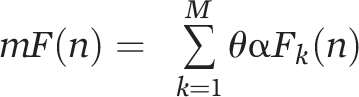 , where θαFk is the frequency of channel k.
, where θαFk is the frequency of channel k.Computation of the Channel Activity Score
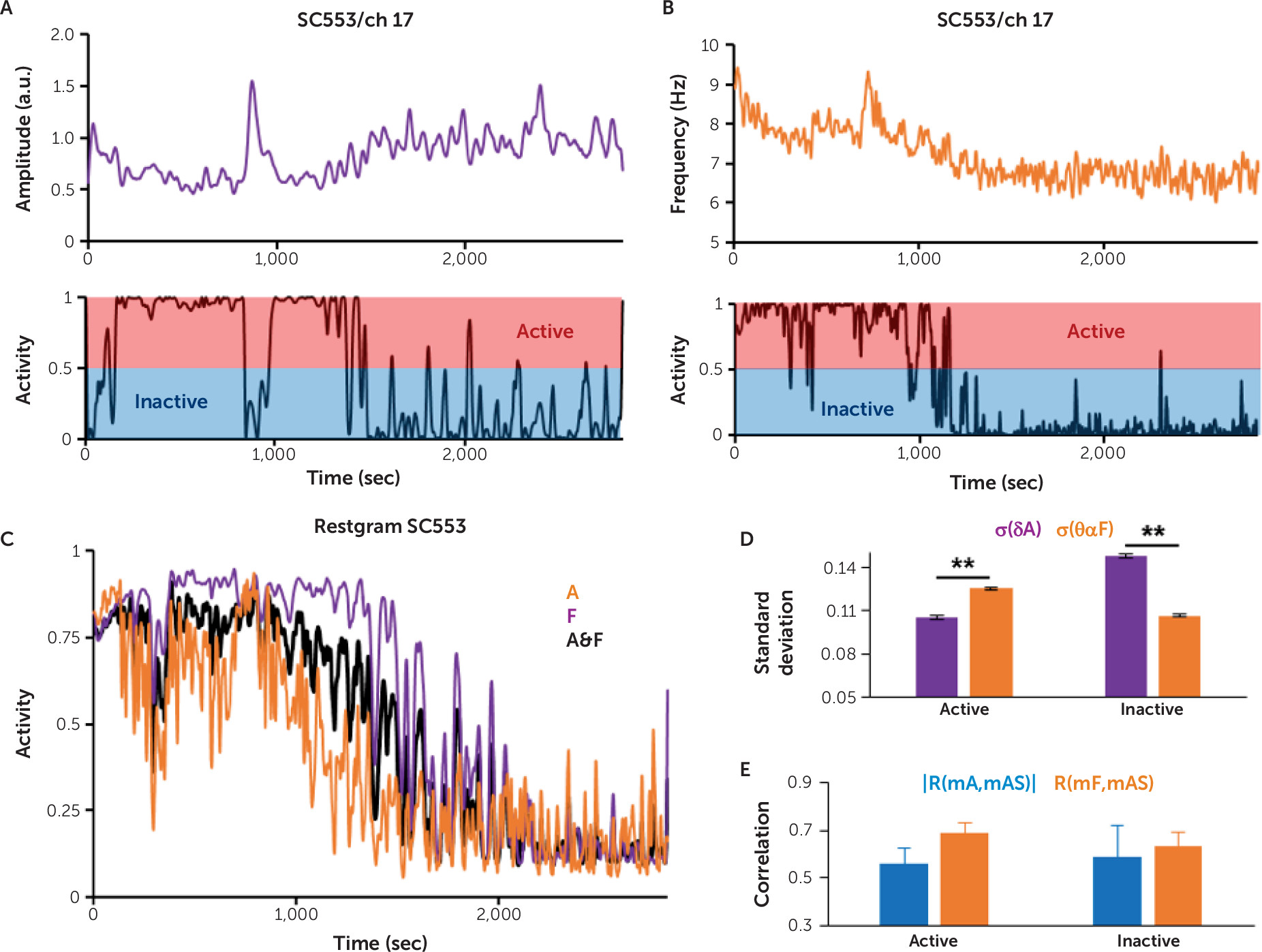
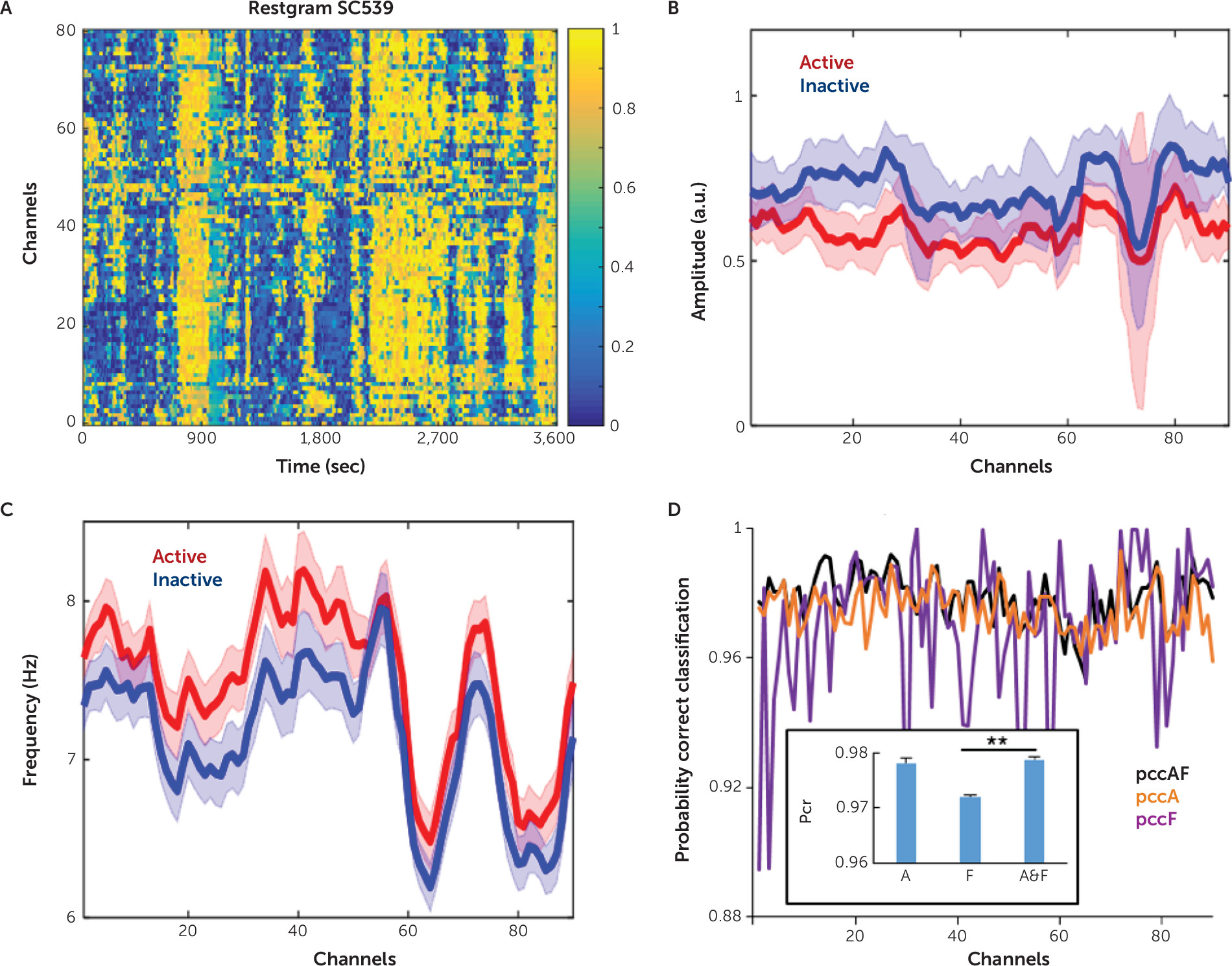
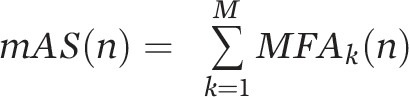 , where MFAk is the activity score of channel k, and n is the time moment (Figure 2C).
, where MFAk is the activity score of channel k, and n is the time moment (Figure 2C).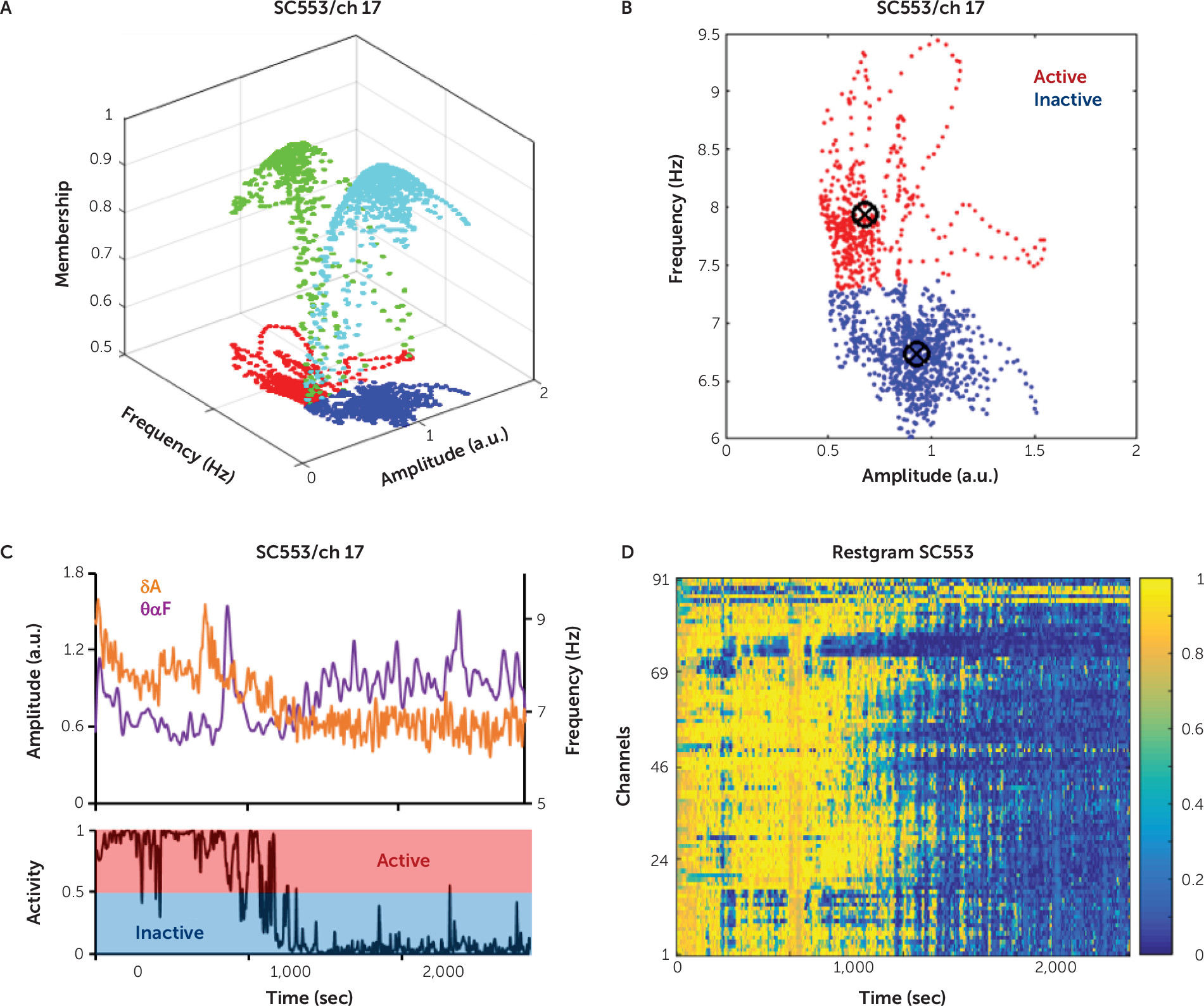
Probability of Correct Classification
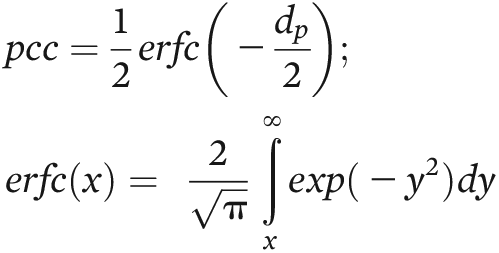
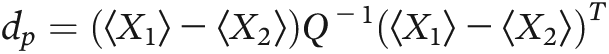
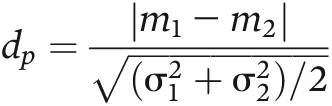
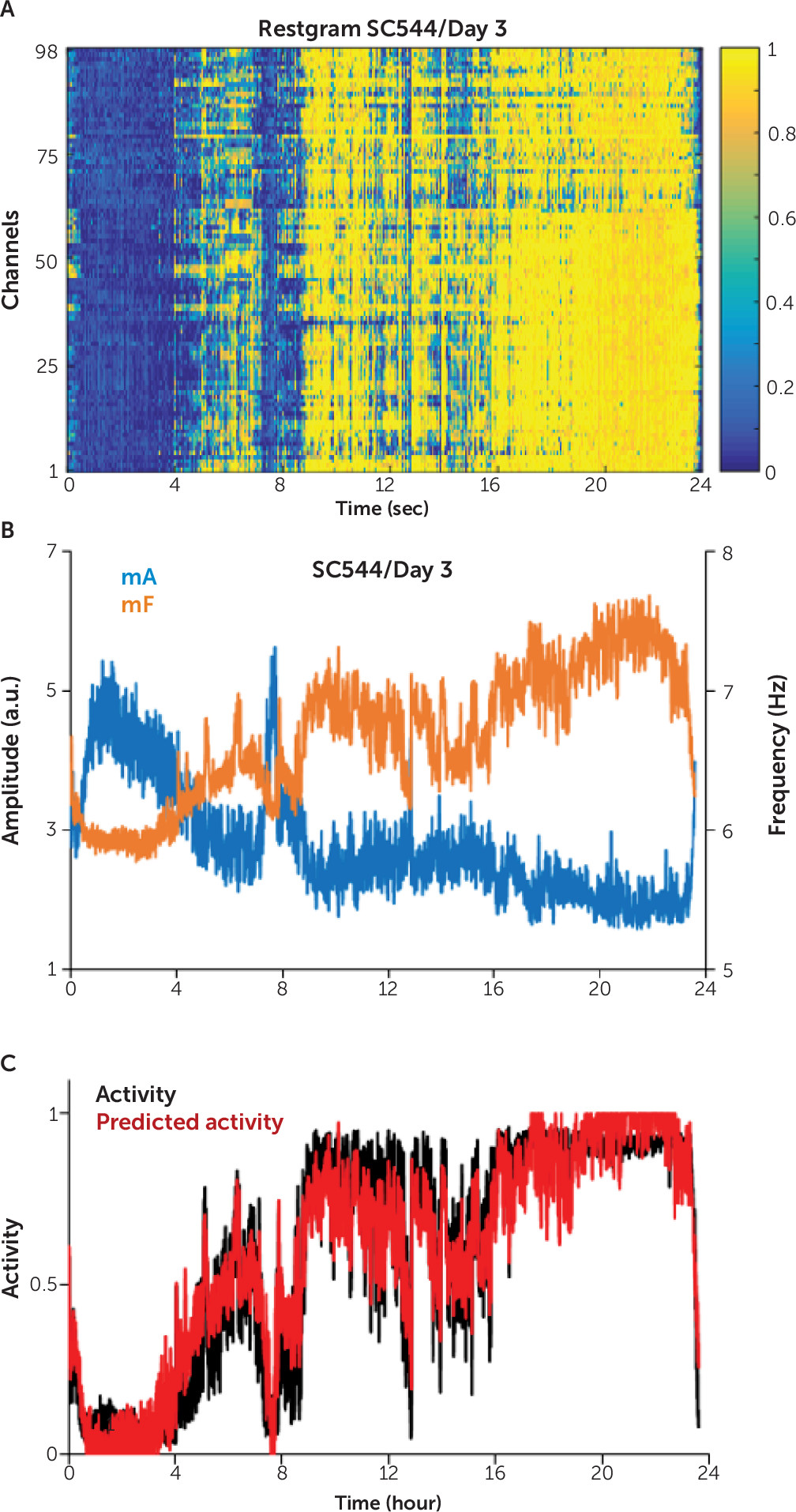
Prediction of the Mean Activity Score
Results
Computing the Channel Activity Score
Comparing Frequency and Amplitude for Activity Classification
Linear Regression Successfully Predicts the Mean Activity Score From the Mean Amplitude and Frequency
Discussion
Conclusions
Footnotes
References
Information & Authors
Information
Published In
History
Keywords
Authors
Competing Interests
Funding Information
Metrics & Citations
Metrics
Citations
Export Citations
If you have the appropriate software installed, you can download article citation data to the citation manager of your choice. Simply select your manager software from the list below and click Download.
For more information or tips please see 'Downloading to a citation manager' in the Help menu.
View Options
View options
PDF/EPUB
View PDF/EPUBLogin options
Already a subscriber? Access your subscription through your login credentials or your institution for full access to this article.
Personal login Institutional Login Open Athens loginNot a subscriber?
PsychiatryOnline subscription options offer access to the DSM-5-TR® library, books, journals, CME, and patient resources. This all-in-one virtual library provides psychiatrists and mental health professionals with key resources for diagnosis, treatment, research, and professional development.
Need more help? PsychiatryOnline Customer Service may be reached by emailing [email protected] or by calling 800-368-5777 (in the U.S.) or 703-907-7322 (outside the U.S.).

