Empirically Derived Decision Trees for the Treatment of Late-Life Depression
Abstract
Objective:
Several predictors of treatment response in late-life depression have been reported in the literature. The aim of this analysis was to develop a clinically useful algorithm that would allow clinicians to predict which patients will likely respond to treatment and thereby guide clinical decision making. Method: A total of 461 patients with late-life depression were treated under structured conditions for up to 12 weeks and assessed weekly with the 17-item Hamilton Rating Scale for Depression (HAM-D-17). The authors developed a hierarchy of predictors of treatment response using signal-detection theory. The authors developed two models, one minimizing false predictions of future response and one minimizing false predictions of future nonresponse, to offer clinicians two clinically useful treatment algorithms. Results: In the first model, early symptom improvement (defined by the relative change in HAM-D-17 total score from baseline to week 4), lower baseline anxiety, and an older age of onset predict response at 12 weeks. In the second model, early symptom improvement represents the principal guide in tailoring treatment, followed by baseline anxiety level, baseline sleep disturbance, and—for a minority of patients—the adequacy of previous antidepressant treatment. Conclusions: Our two models, developed to help clinicians in different clinical circumstances, illustrate the possibility of tailoring the treatment of late-life depression based on clinical characteristics and confirm the importance of early observed changes in clinical status.
(Reprinted with permission from Am J Psychiatry 2008; 165:855–862)
Late-life major depression is associated with emotional suffering, disability, caregiver strain, suicide, and poor compliance with other medical treatments (1). Successful antidepressant treatment is one of the most effective ways to reduce disability, prevent morbidity, and improve quality of life in an older depressed patient (2, 3). In many cases, patients appear to be resistant to treatment because their antidepressants are switched prematurely (4, 5). If treating clinicians knew the probability of treatment response earlier in the course of treatment, they would be in a better position to advise patients about various treatment options. These options could include continuing the current medication, augmenting current pharmacotherapy, or switching to another approach (6, 7).
Previously, our group has shown that a patient's clinical status after 4 weeks of treatment predicts reliably their response status at week 12 (6). Furthermore, we have identified several biological, clinical, and psychosocial characteristics as predictors of treatment response in late-life major depression: allelic variation in the serotonin transporter promoter, REM sleep latency, cerebral glucose metabolism, age at onset of first episode, sleep disturbances at baseline, baseline Hamilton Depression Rating Scale (HAM-D) scores, baseline anxiety levels, suicidal ideation, response and adherence to previous antidepressant treatment, family support, and social inequalities (7–17). To our knowledge, there is no published report of a treatment decision tree based on a hierarchy of factors integrating various predictors of response in acute treatment of late-life major depression. Because most clinicians have access only to clinical variables, we conducted an analysis to integrate and develop a hierarchy of the previously identified clinical predictors. Our aim is to offer clinicians a strategy to tailor treatment planning based on patients' characteristics, thereby developing more successful treatment strategies for late-life major depression.
METHOD
This analysis used pooled data from the acute treatment phase of three previously described treatment studies funded by the National Institute of Mental Health of geriatric depression (18–20). These studies were conducted by the same study personnel in the same university-based research center (21). Comparable inclusion and exclusion criteria as well as assessment and treatment procedures were followed during the acute treatment phase for the three studies.
SUBJECTS
A study of maintenance therapies in recurrent major depression (maintenance therapies in late-life depression 1) provided 168 subjects age 59 and over with recurrent nonpsychotic major depression to this analysis (18). A second maintenance study (maintenance therapies in late-life depression 2) provided 183 subjects age 69 and over with either a single or recurrent nonpsychotic depressive episode (20). The third study, which compared two active drugs in the treatment of late-life major depression (double-blind randomized comparison of nortriptyline and paroxetine in late-life depression) provided an additional 110 subjects age 60 and over with either a single or recurrent nonpsychotic depressive episode (19).
ASSESSMENTS
INCLUSION CRITERIA
All studies required that subjects have a current episode of nonpsychotic unipolar major depression. In maintenance therapies in late-life depression 1, diagnoses were based on the Research Diagnostic Criteria, as established by structured interview with the Schedule for Affective Disorders and Schizophrenia—Lifetime Version (25). In maintenance therapies in late-life depression 2 and double-blind randomized comparison of nortriptyline and paroxetine in late-life depression, diagnoses were based on the criteria of DSM-IV established with the Structured Clinical Interview for DSM-IV Axis I Disorders—Patient Edition (26). Inclusion criteria also required the following baseline scores: HAM-D-17≥17 in maintenance therapies in late-life depression 1 and ≥15 in maintenance therapies in late-life depression 2 and the double-blind randomized comparison of nortriptyline and paroxetine in late-life depression; MMSE ≥27, ≥18, and ≥15 for maintenance therapies in late-life depression 1, maintenance therapies in late-life depression 2, and double-blind randomized comparison of nortriptyline and paroxetine in late-life depression, respectively.
ACUTE TREATMENT PROTOCOLS
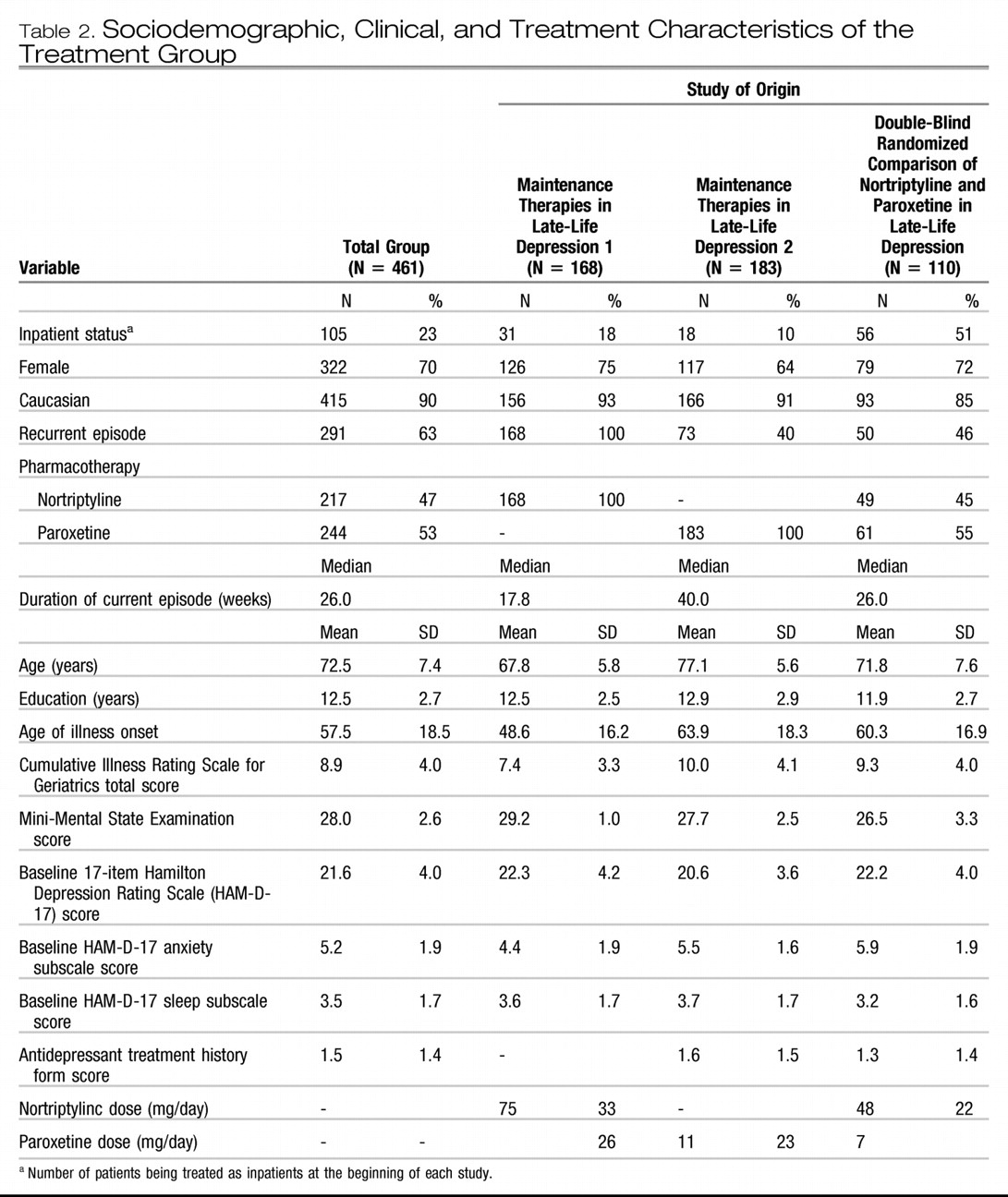
During the acute phase of maintenance therapies in late-life depression, the subjects were treated openly with nortriptyline titrated to yield a plasma level of 80–120 ng/ml, combined with weekly interpersonal therapy. During the acute phase of treatment in maintenance therapies in late-life depression 2, the subjects were treated openly with paroxetine in doses adjusted between 10 and 40 mg/day based on tolerability and response (mean [SD] final dose: 26 (11) mg/day), combined with weekly interpersonal therapy. In the double-blind randomized comparison of nortriptyline and paroxetine in late-life depression, the subjects were randomly assigned to blinded treatment with nortriptyline or paroxetine. Nortriptyline dose was titrated to a plasma level of 50–120 ng/ml. Paroxetine doses were adjusted between 10 and 40 mg/day based on tolerability and response (mean [SD] final dose: 23 (7) mg/day). All three studies included dosing strategies to optimize both treatment response and tolerability.
As described elsewhere, we pooled data from the three studies to obtain a heterogeneous sample representative of depressed elderly seeking treatment (6). The subjects who did not respond to their initial treatment were eligible to receive augmentation pharmacotherapy in maintenance therapies in late-life depression 1 and 2. In the double-blind randomized comparison of nortriptyline and paroxetine in late-life depression, the subjects who did not respond to their randomized treatment could be switched to the alternative drug. For this analysis, the subjects who did not receive monotherapy with their initial antidepressant medication for a full 12 weeks were censored at the time of augmentation or medication switch, and we used imputed values for the remaining period (see below). As a result, observed HAM-D scores were available for 461 subjects at baseline, 373 at week 4, and 247 at week 12. Imputations were performed for both intermittent missing and monotone missing observations (6). Intermittent missing refers to occasions when the missing observations are preceded and succeeded by observations (e.g., when data were not available during 1 week but were available for the preceding and following weeks). Monotone missing observations have no further observation, for example, due to withdrawing consent and dropping out of the study or to censoring at the time of initiation of adjunctive treatment or of switching medications. For this analysis, multiple imputations were performed using the Markov Chain Monte Carlo option of the multiple imputation procedure (PROC MI) in the SAS software (27). A detailed description of the Markov Chain Monte Carlo can be found in a previous report (6).
For all analyses, response was defined categorically as both a decrease in a HAM-D score of 50% or more from baseline and a score of 10 or less. 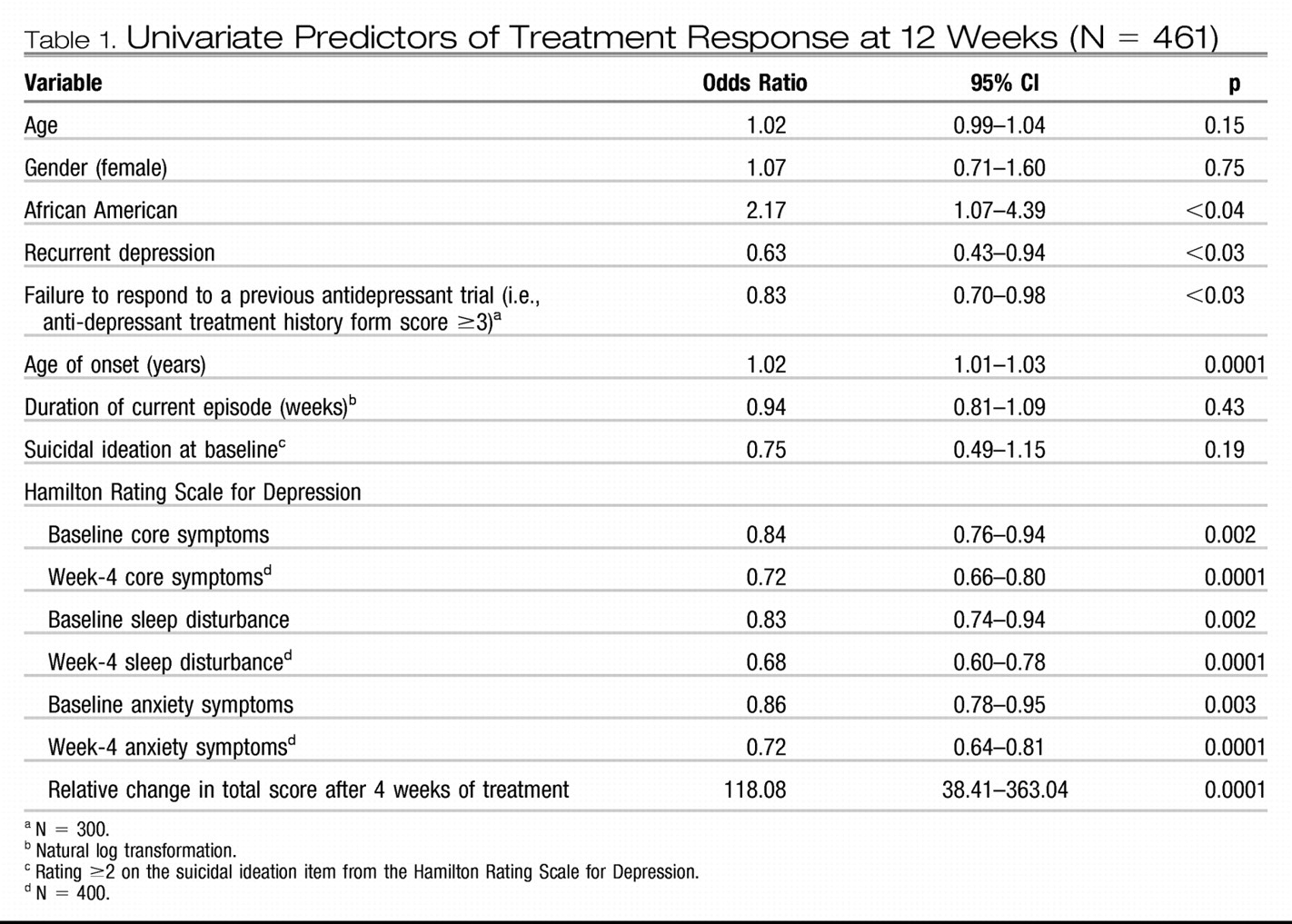Based on our previous work, we defined core HAM-D symptoms as HAM-D items 1, 2, 3, and 7 (depressed mood, guilt, suicide, and work/activities); anxiety HAM-D symptoms as items 9, 10, 11, and 15 (agitation, psychic anxiety, somatic anxiety, and hypochondriasis); and sleep HAM-D symptoms as items 4, 5, and 6 (early, middle, and late insomnia) (28). We initially performed a univariate logistic regression on the demographic and clinical variables to identify potential predictors of treatment response. Response at 12 weeks was the binary dependent variable (Table 1). Subsequently, to obtain a hierarchy of these predictors, we incorporated these potential predictors in a receiver-operating characteristic model using signal detection theory as described by Kiernan at al (29).
a N = 300.
b Natural log transformation.
c Rating ≥2 on the suicidal ideation item from the Hamilton Rating Scale for Depression.
d N = 400.
Signal detection theory has been especially useful in analyses where predictors are likely to be highly collinear and interactions between independent variables exist (29). In our case, the signal is a binary outcome (response/nonresponse at 12 weeks) and the detection is for the set of predictor variables (29). Signal detection identifies predictors with a stopping rule of p <0.05. The highest predicting variable is used to divide the sample into two subsamples, and the next predicting variable divides the higher-risk subsample. The process continues until the lowest risk variable stops at p <0.05 (29). Variables associated with a p >0.05 are excluded from the decision tree. Signal detection determines the optimal cutoff point across all increments of a variable and across all variables (29).
We built two different models by modulating the sensitivity threshold for each predictor of treatment response to obtain hierarchies of risk correlated with different patients' characteristics.
First, a low sensitivity threshold was used to define a model that minimizes false positives. A high rate of false positives (i.e., falsely predicting that patients will respond to treatment) could lead clinicians to continue a treatment that will eventually be ineffective. Avoiding this results in an aggressive treatment approach that clinicians might consider appropriate in various clinical situations (including but not limited to patients who have a higher risk of suicide or who are severely disabled by their depression).
Second, we used a high sensitivity threshold to define a model that minimizes false negatives. A high rate of false negatives (i.e., falsely predicting that a patient will be a nonresponder) could lead clinicians either to use unnecessary augmentation pharmacotherapy (thus exposing the patient to the risk of adverse effects) or to switch prematurely to another antidepressant (thus depriving patients from eventually responding to the first agent). Avoiding premature treatment changes results in a conservative approach (appropriate in various clinical situations, including but not limited to patients who have a history of multiple unsuccessful trials). In light of the results of the STAR-D study, emphasizing how long it can take to identify an effective treatment (30, 31), it is important not to “miss” an effective treatment because of a premature switch.
For the first model (minimizing false positives), we used a sensitivity cutoff point of 0.3. For the second model (minimizing false negatives), we used a sensitivity cutoff point of 0.7 (32). The selection of variables was based upon the univariate regression results and available sample. The potential predictors included race, age of onset, recurrence, baseline sleep disturbance, baseline anxiety, and early symptom improvement. Early symptom improvement was defined by the percent decrease in HAM-D score achieved by week 4. However, because clinicians do not use cutoff points such as those generated by the model, we converted the percentage cutoffs to corresponding clinical changes. Thus, we considered a decrease in HAM-D score of more than 45% at week 4 as a marked early improvement, a decrease of HAM-D score between 30% and 45% as a moderate early improvement, a decrease in HAM-D score between 18% and 30% as a mild early improvement, and a decrease of HAM-D of less than 18% as the absence of clinically noticeable improvement, i.e., a poor early improvement.
We used the antidepressant treatment history form to assess the adequacy of all the antidepressant trials received during the current episode based on both the duration and the dose of treatment. The antidepressant treatment history form scores are ordinal: 1 (definitely inadequate = trial of less than 4 weeks or of more than 4 weeks with a very low dose), 2 (probably inadequate = a trial of more than 4 weeks with probably inadequate doses), 3 (probably adequate = a trial of more than 4 weeks of an antidepressant at an adequate dose), 4 (definitely adequate = a trial longer than 4 weeks with intensive doses of antidepressant), or 5 (definitely adequate antidepressant with lithium augmentation). Antidepressant treatment history form scores were available for a subgroup of patients (N = 289), and we repeated the analysis in this subgroup using the highest scores—corresponding to the strongest previous treatment trial the patient had failed to respond to during the current episode—as had been done in several previous analyses (33, 34).
RESULTS
Table 2 presents the baseline demographic and clinical characteristics of the subjects from each of the three studies and of the pooled study group. Table 1 presents the results of the univariate logistic regression.
a Number of patients being treated as inpatients at the beginning of each study.
AGGRESSIVE TREATMENT APPROACH
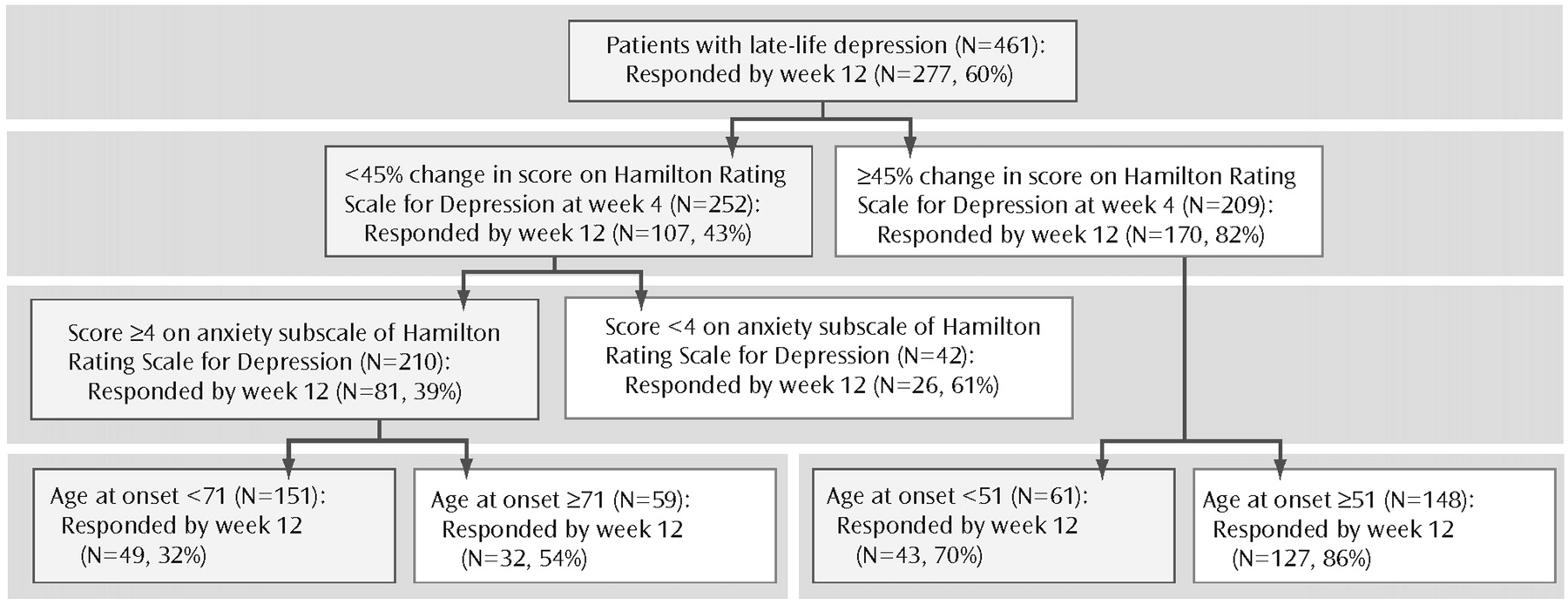
In the first predictor of treatment results model, we set the sensitivity cutoff point at 0.3 to minimize false positives. In this model, the significant predictors of treatment response by week 12 were early symptom improvement, higher baseline anxiety, and younger age of onset in this ranking order (Figure 1). The other variables included in the model did not exceed the cutoff point of 0.05.
a
Main outcome = full response status at week 12. Proportion of responders at 12 weeks = 60%. A change in Hamilton Rating Scale for Depression score at week 4 of less than 45% from baseline predicts a less than half (43%) chance of responding at week 12. For the patients in this group, higher baseline anxiety predicts a 39% chance of responding at week 12. For patients with higher baseline anxiety, a younger age of onset predicts a 32% chance of responding at week 12.
As illustrated in Figure 1, if a patient has a moderate early improvement, his chances of achieving a full response at week 12 are 43%, whereas if a patient has a marked early improvement, his chances of achieving a full response at week 12 are 82%. For the subjects with only a moderate early improvement, the next predictor influencing the likelihood of response is the level of baseline anxiety; a high baseline anxiety (HAM-D anxiety subscale ≥4) predicts a chance of response of 39% at week 12, whereas a low baseline anxiety improves that chance to 61%. For the subjects with only a moderate early improvement and high baseline anxiety, the next variable that weighs in predicting treatment response is age of onset. Older age of onset correlates with higher chance of response (54%), whereas younger age of onset correlates with a poorer chance of response (33%) (Figure 1).
We introduced the adequacy of previous treatment (antidepressant treatment history form score) into the same model, but the antidepressant treatment history form score does not constitute a significant predictor in this model (data not shown).
CONSERVATIVE TREATMENT APPROACH
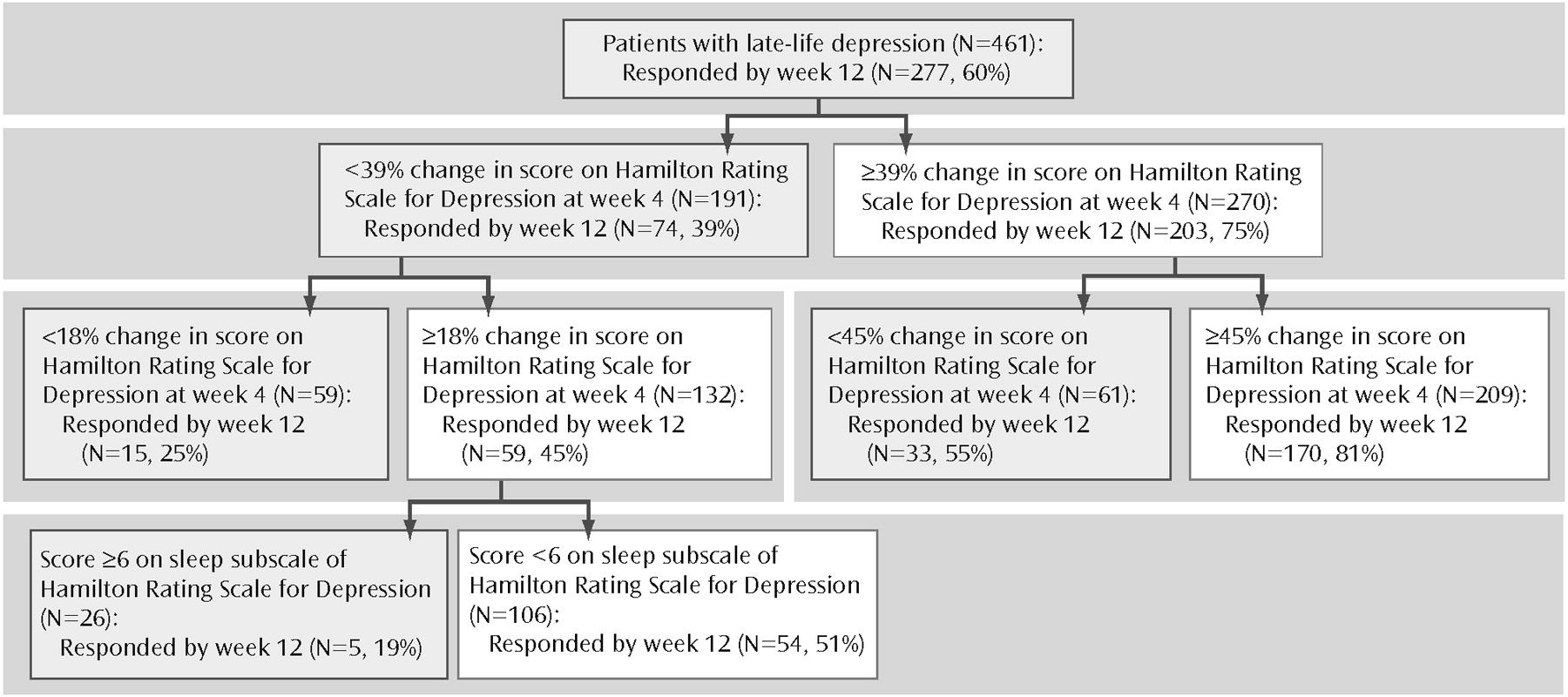
In the second predictor of treatment response model, we set the sensitivity cutoff point at 0.7 to minimize false negatives. In this model, the significant predictors of treatment response by week 12 were early symptom improvement and sleep disturbance. Early symptom improvement is both the first- and second-tier variable, whereas baseline sleep disturbance is a third-tier predictor of treatment response for patients who had at least a mild early improvement. Thus, for a patient with at least a mild early improvement, high baseline sleep disturbance predicts a 19% chance of full response at 12 weeks, whereas low baseline sleep disturbance predicts a 51% chance of full response by 12 weeks (Figure 2).
a
Main outcome = full response status at week 12. Proportion of responders at 12 weeks = 60%. A change in Hamilton Rating Scale for Depression score at week 4 is the main predictor of treatment response in this model. A change of less than 39% from baseline predicts a 39% chance of responding at week 12, followed by a change of less than 18% from baseline, predicting a 25% chance of responding at week 12. For the subjects with an 18% or higher change in Hamilton Rating Scale for Depression score at week 4, higher baseline sleep disturbance predicts a 19% chance of responding at week 12.
If we introduce the adequacy of previous treatment in this second model, we obtain a different hierarchy of risks: although early symptom improvement remains the highest-ranking predictor, the adequacy of previous antidepressant trials and baseline anxiety constitute the secondtier predictors. Thus, patients with minimal early symptom improvement who have received inadequate antidepressant treatment before study participation have a 45% chance of becoming full responders at week 12, whereas those who had received adequate trials of antidepressant pharmacotherapy have only a 13% chance of becoming full responders at week 12. We suggest that this last profile represents a subgroup of treatment-resistant subjects.
In contrast to patients with only a mild early improvement, patients with at least a moderate early improvement have a 73% chance of achieving a full response. Further-more, for these patients, the adequacy of previous trials is not a significant predictor. In this case, the second-tier predictor of treatment response is baseline anxiety. High baseline anxiety (HAM-D anxiety subscale score ≥8) lowers the chances of achieving a full response to 40%, whereas low baseline anxiety increases the chances of achieving a full response to 79% (Figure 3).
a
Main outcome = full response status at week 12. Proportion of responders at 12 weeks = 64%. For the antidepressant treatment history form, a score of ≥3 = probably adequate antidepressant treatment history (trial of more than 4 weeks of an antidepressant at an adequate dose). For the antidepressant treatment history form a score of <3 = inadequate antidepressant history (trial of less than 4 weeks or of more than 4 weeks but with an inadequate dose). High anxiety = at least moderate anxiety symptoms. Low anxiety = mild or no anxiety symptoms. Change in Hamilton Rating Scale for Depression (HAM-D) at week 4 of less than 30% from baseline predicts a 36% chance of responding at week 12. For the subjects with a lower than 30% change in HAM-D score at week 4, a history of at least one adequate antidepressant trial predicts a 14% chance of responding at week 12. For the subjects with a 30% or higher change in HAM-D at week 4, the next predictor of treatment response is baseline anxiety. A higher baseline anxiety score predicts a lower chance of responding at 12 weeks (41%), whereas a lower baseline anxiety score predicts a 79% chance of responding at week 12.
DISCUSSION
Our analysis confirms that demographic and clinical variables can be used to predict treatment response and guide treatment decision in late-life major depression. The group of predictors of treatment response identified by our univariate logistic regression is congruent with the previous literature reporting on the contribution of several demographic and clinical factors in predicting treatment response in late-life major depression (7, 9–11). Using signal detection theory, we identified the hierarchy of predictors of treatment response in two decision tree models.
In the first model—corresponding to an aggressive treatment approach in situations when long treatment trials that are eventually unsuccessful are particularly undesirable—the most important predictor of treatment response at 12 weeks is early symptom improvement. Thus, early symptom improvement “trumps” the predictive power of all other variables, and it is the most important variable in adjusting treatment decisions, followed by the presence at baseline of at least mild to moderate anxiety symptoms. This is congruent with results reported previously by our group (6, 7).
To translate this model in clinical terms, we may consider the case of a 65-year-old inpatient with major depression who, after 4 weeks of treatment, experienced moderate symptom improvement. This already tells the clinician that the patient has less than half (43%) a chance of becoming a full responder if the course of treatment remains unchanged for the entire 12 weeks. If the patient had minimal anxiety at baseline, the clinician might decide at this point to continue the current treatment because low baseline anxiety increases the patient's chances of becoming a full responder from 43% to 61%. But if this patient also started with moderate or high anxiety, her chances of responding have further decreased to 39%. Moreover, an earlier age of onset would put this patient in the worst-prognosis category, with a further decline of her chances of being a full responder at 12 weeks to 33%. In this case, rather than waiting for a full 12 weeks, the best clinical decision would be to attempt a different treatment course (e.g., switch or augmentation).
In the second model—consistent with a conservative treatment in situations when concluding prematurely and wrongly that a specific antidepressant is ineffective is particularly undesirable—the most important predictor of treatment response at 12 weeks remains the early symptom improvement, followed by severe sleep disturbance at baseline. If we incorporate the adequacy of previous antidepressant trials in this model, early symptom improvement remains the most important predictor of treatment response with adequacy of previous treatment becoming a second-ranked variable.
To translate this model in clinical terms, we can consider the case of a 65-year-old outpatient with major depression and a history of multiple unsuccessful antidepressant trials. After 4 weeks of treatment with a new drug, he experienced a moderate improvement of his symptoms. Based on our model for this clinical situation, the patient has less than a 39% chance of becoming of full responder if the course of treatment remains unchanged for the entire 12 weeks. If the clinician does not have an accurate treatment history of his patient, the only other clinical characteristic important in reaching a treatment decision at this point is the patient's baseline sleep. If the patient did not have severe baseline sleep disturbances, his chances of becoming a full responder at 12 weeks with the current treatment are less than one in five (19%). In this case, the clinician would probably consider changing the course of the treatment at week 4. However, if the patient did not have severe sleep disturbances at baseline, he has a 51% chance of becoming a full responder at 12 weeks. At this point, this model would allow the clinician to present to his patient an informal estimate of his chances of recovery and decide together with the patient the best course of action.
For the same patient, if the clinician has an accurate treatment history showing he never received an adequate trial of antidepressant during this depressive episode, the chances the patient has of becoming a full responder at 12 weeks are 46%. Because his chances of response are less than half with the current treatment, it probably makes more sense for the clinician to consider augmenting or switching treatment at this point.
Overall, instead of impressionistic-based clinical decisions, these models provide clinicians with a potentially useful tool for navigating the maze of multiple clinical predictors. They allow clinicians to adapt their decisions to the specific clinical characteristics encountered when treating an elderly patient with depression. These models also emphasize the importance of measure-based treatment approaches (e.g., the HAM-D) to monitor treatment response. In a managed-care environment, it is difficult to use time-consuming questionnaires routinely. However, using the HAM-D or a self-rated scale such as the Beck Depression Inventory (35) twice (at baseline and week 4) could save time and clinical effort.
This analysis has several strengths, including a relatively large sample. Despite a dropout rate of 48%, this sample size combined with an imputation model allowed us to identify second- and third-ranked predictors of treatment response. In addition, we examined two models that correspond to different treatment strategies. The limitation of this analysis includes the data pooling across three different studies with different entry criteria and different treatments. However, in an additional analysis, specific studies were not found to be predictors of outcome in either model (data not shown). Moreover, these differences enhance the generalizability of our findings. Our data were collected in patients receiving structured treatment, including weekly clinical monitoring. Thus, the course of symptom resolution we observed might represent what happens under optimal conditions rather than what typically happens under “usual care” conditions (36). By design, this analysis focuses on the outcome of first-line pharmacotherapy. Consequently, our models do not elucidate the role of augmentation or switching. However, our group has recently addressed the outcomes of augmentation strategies using a different analytical model (37, 38).
We could not include the antidepressant treatment history form variable in the main model because it was collected only for a subgroup of patients. Thus, we had less power to determine the extent to which adequacy of previous treatment is a predictor of treatment response. Most of our patients were Caucasians; therefore, our findings cannot be generalized to other ethno-racial groups.
In conclusion, our two models can improve the precision of clinical predictions based on a few clinical variables. Future work should assess whether these predictions can be refined further by combining clinical and biological variables (39). In particular, the inclusion of specific biomarkers might extend our predictive ability beyond the current estimates and would improve the development and monitoring of tailored treatments.
Acknowledgments
Dr. Whyte has received research support from NIMH, Forest, Ortho-McNeil, and Pfizer, Dr. Mazumdar owns stock in Forest (less than $10,000). Dr. Mulsant has received research support or honoraria from AstraZeneca, Bristol-Myers Squibb, Eli Lilly, Forest, GlaxoSmithKline, Janssen, Lundbeck, NIH, Corcept, Elsai, and Pfizer; he holds stock (all less than $10,000) in Akzo-Nobel, Alkermes, AstraZeneca, Biogen Idec, Celsion, Elan, Eli Lilly, Forest, Orchestra Therapeutics, General Electric, Immune Response, and Pfizer. He has been a consultant to AstraZeneca, Bristol-Myers Squibb, Elsai, Eli Lilly, Forest, Fox Learning System, GlaxoSmithKline, Janssen, Lundbeck, and Pfizer. He has been on the speakers bureaus of AstraZeneca, Elsai, Forest, GlaxoSmithKline, Janssen, and Pfizer. He has received other financial support from Forest and Janssen. Dr. Pollock has received honoraria and/or research support from Janssen Pharmaceutica, Forest, NIH, GlaxoSmithKline, and Solvay and is on the speakers bureau for Forest and Sepracor. He has been on the advisory boards of Forest and is a faculty member of Lundbeck Institute. Dr. Reynolds has received research support from GlaxoSmithKline, Pfizer, Eli Lilly, Bristol-Myers Squibb, and Forest. The remaining authors report no competing interests.
REFERENCES
1.
Charney DS, Reynolds CF III, Lewis L, Lebowitz BD, Sunderland T, Alexopoulos GS, Blazer DG, Katz IR, Meyers BS, Arean PA, Borson S, Brown C, Bruce ML, Callahan CM, Charlson ME, Conwell Y, Cuthbert BN, Devanand DP, Gibson MJ, Gottlieb GL, Krishnan KR, Laden SK, Lyketsos CG, Mulsant BH, Niederehe G, Olin JT, Oslin DW, Pearson J, Persky T, Pollock BG, Raetzman S, Reynolds M, Salzman C, Schultz R, Schwenk TL, Scolnick E, Unutzer J, Weissman MM, Young RC, Depression and Bipolar Support Alliance: Depression and Bipolar Support Alliance consensus statement on the unmet needs in diagnosis and treatment of mood disorders in late life. Arch Gen Psychiatry 2003; 60: 664– 672
2.
Dombrovski AY, Mulsant BH, Houck PR, Mazumdar S, Lenze EJ, Andreescu C, Cyranowski JM, Reynolds CF III: Residual symptoms and recurrence during maintenance treatment of latelife depression. J Affect Disord 2007; 103: 77– 82
3.
Mulsant BH, Pollock BG: Treatment-resistant depression in late life. J Geriatr Psychiatry Neurol 1998; 11: 186– 193
4.
Mulsant BH, Whyte E, Lenze EJ, Lotrich F, Karp JF, Pollock BG, Reynolds CF III: Achieving long-term optimal outcomes in geriatric depression and anxiety. CNS Spectr 2003; 8( 12 suppl 3): 27– 34
5.
Guscott R, Grof P: The clinical meaning of refractory depression: a review for the clinician. Am J Psychiatry 1991; 148: 695– 704
6.
Mulsant BH, Houck PR, Gildengers AG, Andreescu C, Dew MA, Pollock BG, Miller MD, Stack JA, Mazumdar S, Reynolds CF III: What is the optimal duration of a short-term antidepressant trial when treating geriatric depression? J Clin Psychopharmacol 2006; 26: 113– 120
7.
Andreescu C, Lenze EJ, Dew MA, Begley AE, Mulsant BH, Dombrovski AY, Pollack BG, Stack J, Miller MD, Reynolds CF: Effect of comorbid anxiety on treatment response and relapse risk in late-life depression: controlled study. Br J Psychiatry 2007; 190: 344– 349
8.
Szanto K, Mulsant BH, Houck P, Dew MA, Reynolds CF III: Occurrence and course of suicidality during short-term treatment of late-life depression. Arch Gen Psychiatry 2003; 60: 610– 617
9.
Dew MA, Reynolds CF III, Houck PR, Hall M, Buysse DJ, Frank E, Kupfer DJ: Temporal profiles of the course of depression during treatment: predictors of pathways toward recovery in the elderly. Arch Gen Psychiatry 1997; 54: 1016– 1024
10.
Gildengers AG, Houck PR, Mulsant BH, Dew MA, Aizenstein HJ, Jones BL, Greenhouse J, Pollack BG, Reynolds CF III: Trajectories of treatment response in late-life depression: psychosocial and clinical correlates. J Clin Psychopharmacol 2005; 25( 4 suppl 1): S8– S13
11.
Tew JD Jr, Mulsant BH, Houck PR, Lenze EJ, Whyte EM, Miller MD, Stack JA, Bensasi S, Reynolds CF III: Impact of prior treatment exposure on response to antidepressant treatment in late life. Am J Geriatr Psychiatry 2006; 14: 957– 965
12.
Lotrich FE, Pollock BG, Ferrell RE: Polymorphism of the serotonin transporter: implications for the use of selective serotonin reuptake inhibitors. Am J Pharmacogenomics 2001; 1: 153– 164
13.
Pollock BG, Ferrell RE, Mulsant BH, Mazumdar S, Miller M, Sweet RA, Davis S, Kirshner MA, Houck PR, Stack JA, Reynolds CF, Kupfer DJ: Allelic variation in the serotonin transporter promoter affects onset of paroxetine treatment response in latelife depression. Neuropsychopharmacology 2000; 23: 587– 590
14.
Reynolds CF III, Hoch CC, Buysse DJ, George CJ, Houck PR, Mazumdar S, Miller M, Pollock BG, Rifai H, Frank E, et al: Sleep in late-life recurrent depression: changes during early continuation therapy with nortriptyline. Neuropsychopharmacology 1991; 5: 85– 96
15.
Smith GS, Reynolds CF III, Pollock B, Derbyshire S, Nofzinger E, Dew MA, Houck PR, Milko D, Meltzer CC, Kupfer DJ: Cerebral glucose metabolic response to combined total sleep deprivation and antidepressant treatment in geriatric depression. Am J Psychiatry 1999; 156: 683– 689
16.
Cohen A, Houck PR, Szanto K, Dew MA, Gilman SE, Reynolds CF III: Social inequalities in response to antidepressant treatment in older adults. Arch Gen Psychiatry 2006; 63: 50– 56
17.
Martine LM, Schulz R, Reynolds CF III, Morse JQ, Butters MA, Hinrichsen GA: Impact of close family members on older adults' early response to depression treatment. Psychol Aging (in press)
18.
Reynolds CF III, Frank E, Perel JM, Imber SD, Cornes C, Miller MD, Mazumdar S, Houck PR, Dew MA, Stack JA, Pollock BG, Kupfer DJ: Nortriptyline and interpersonal psychotherapy as maintenance therapies for recurrent major depression: a randomized controlled trial in patients older than 59 years. JAMA 1999; 281: 39– 45
19.
Mulsant BH, Pollock BG, Nebes R, Miller MD, Sweet RA, Stack J, Houck PR, Bensasi S, Mazumdar S, Reynolds CD III: A twelve-week, double-blind, randomized comparison of nortriptyline and paroxetine in older depressed inpatients and outpatients. Am J Geriatr Psychiatry 2001; 9: 406– 414
20.
Reynolds CF III, Dew MA, Pollock BG, Mulsant BH, Frank E, Miller MD, Houck PR, Mazumdar S, Butters MA, Stack JA, Schlernitzauer MA, Whyte EM, Gildengers A, Karp J, Lenze E, Szanto K, Bensasi S, Kupfer DJ: Maintenance treatment of major depression in old age. N Engl J Med 2006; 354: 1130– 1138
21.
Gildengers AG, Houck PR, Mulsant BH, Pollock BG, Mazumdar S, Miller MD, Dew MA, Frank E, Kupfer DJ, Reynolds CF III: Course and rate of antidepressant response in the very old. J Affect Disord 2002; 69: 177– 184
22.
Hamilton M: A rating scale for depression. J Neurol Neurosurg Psychiatry 1960; 23: 56– 62
23.
Folstein MF, Folstein SE, McHugh PR: “Mini-Mental State”: a practical method for grading the cognitive state of patients for the clinician. J Psychiatr Res 1975; 12: 189– 198
24.
Miller MD, Paradis CF, Houck PR, Mazumdar S, Stack JA, Rifai AH, Mulsant B, Reynolds CF III: Rating chronic medical illness burden in geropsychiatric practice and research: application of the Cumulative Illness Rating Scale. Psychiatry Res 1992; 41: 237– 248
25.
Endicott J, Spitzer RL: A diagnostic interview. Arch Gen Psychiatry 1978; 35: 837– 844
26.
First MB, Spitzer RL, Williams JBW, Gibbon M: Structured Clinical Interview for DSM-IV Axis I Disorders—Patient Edition (SCID-P). Washington, DC, American Psychiatric Press, 1995
27.
SAS Institute. SAS/STAT Software, Version 8. Cary, NC, SAS Institute, 2000
28.
Dombrovski AY, Blakesley-Ball RE, Mulsant BH, Mazumdar S, Houck PR, Szanto K, Reynolds CF III: Speed of improvement in sleep disturbance and anxiety compared with core mood symptoms during acute treatment of depression in old age. Am J Geriatr Psychiatry 2006; 14: 550– 554
29.
Kiernan M, Kraemer HC, Winkleby MA, King AC, Taylor CB: Do logistic regression and signal detection identify different sub-groups at risk? implications for the design of tailored interventions. Psychol Methods 2001; 6: 35– 48
30.
Trivedi MH, Rush AJ, Wisniewski SR, Nierenberg AA, Warden D, Ritz L, Norquist G, Howland RH, Lebowitz B, McGrath PJ, Shores-Wilson K, Biggs MM, Balasubramani GK, Fava M, STAR-D Study Team: Evaluation of outcomes with citalopram for depression using measurement-based care in STAR*D: implications for clinical practice. Am J Psychiatry 2006; 163: 28– 40
31.
Fava M, Rush AJ, Wisniewski SR, Nierenberg AA, Alpert JE, McGrath PJ, Thase ME, Warden D, Biggs M, Luther JF, Niederehe G, Ritz L, Trivedi MH: A comparison of mirtazapine and nortriptyline following two consecutive failed medication treatments for depressed outpatients: a STAR*D report. Am J Psychiatry 2006; 163: 1161– 1172
32.
Signal Detection or ROC Software. http://mirecc.stanford.edu
33.
Andreescu C, Mulsant BH, Peasley-Miklus C, Rothschild AJ, Flint AJ, Heo M, Caswell M, Whyte EM, Meyers BS, STOP-PD Study Group: Persisting low use of antipsychotics in the treatment of major depressive disorder with psychotic features. J Clin Psychiatry 2007; 68: 194– 200
34.
Oquendo MA, Baca-Garcia E, Kartachov A, Khait V, Campbell CE, Richards M, Sackeim HA, Prudic J, Mann J: A computer algorithm for calculating the adequacy of antidepressant treatment in unipolar and bipolar depression. J Clin Psychiatry 2003; 64: 825– 833
35.
Beck AT, Ward CH, Mendelson M, Mock J, Erbaugh J: An inventory for measuring depression. Arch Gen Psychiatry 1961; 4: 53– 63
36.
Meyers BS, Sirey JA, Bruce M, Hamilton M, Raue P, Friedman SJ, Rickey C, Kakuma T, Carroll MK, Kiosses D, Alexopoulos G: Predictors of early recovery from major depression among persons admitted to community based clinics: an observational study. Arch Gen Psychiatry 2002; 59: 729– 735
37.
Dew MA, Whyte EM, Lenze EJ, Houck PR, Mulsant BH, Pollock BG, Stack JA, Bensasi S, Reynolds CF III: Recovery from major depression in older adults receiving augmentation of antidepressant pharmacotherapy. Am J Psychiatry 2007; 164: 892– 899
38.
Whyte EM, Basinski J, Farhi P, Dew MA, Begley A, Mulsant BH, Reynolds CF: Geriatric depression treatment in nonresponders to selective serotonin reuptake inhibitors. J Clin Psychiatry 2004; 65: 1634– 1641
39.
Lenze EJ, Mulsant BH: Biomarkers in geriatric psychiatry. Am J Geriatr Psychiatry 2007; 15: 827– 831
Information & Authors
Information
Published In
History
Published online: 1 January 2009
Published in print: Winter 2009
Authors
Metrics & Citations
Metrics
Citations
Export Citations
If you have the appropriate software installed, you can download article citation data to the citation manager of your choice. Simply select your manager software from the list below and click Download.
For more information or tips please see 'Downloading to a citation manager' in the Help menu.
View Options
View options
PDF/EPUB
View PDF/EPUBGet Access
Login options
Already a subscriber? Access your subscription through your login credentials or your institution for full access to this article.
Personal login Institutional Login Open Athens loginNot a subscriber?
PsychiatryOnline subscription options offer access to the DSM-5-TR® library, books, journals, CME, and patient resources. This all-in-one virtual library provides psychiatrists and mental health professionals with key resources for diagnosis, treatment, research, and professional development.
Need more help? PsychiatryOnline Customer Service may be reached by emailing [email protected] or by calling 800-368-5777 (in the U.S.) or 703-907-7322 (outside the U.S.).