Objective: Second-generation antipsychotics make up one of the fastest growing segments of the rapidly growing pharmaceutical sector. Given limited health care resources, assessment of the value for the cost of second-generation antipsychotics relative to first-generation antipsychotics is critical for resource-allocation decisions. Method: With a MEDLINE search, the authors identified eight studies (based on six randomized clinical trials) that analyzed the cost-effectiveness of second-generation antipsychotics relative to first-generation antipsychotics in individuals with schizophrenia disorders. The authors reviewed appropriate methods of measurement, analysis, and design of cost-effectiveness studies in randomized clinical trials and evaluated the validity of economic results derived from the studies in light of appropriate methods. Results: The eight randomized clinical trial-based cost-effectiveness studies of antipsychotic medications faced a variety of threats to validity related to 1) measurement of costs, 2) measurement of effectiveness, 3) analysis of costs, 4) measurement of sampling uncertainty, 5) analysis of incomplete cost data, 6) minimizing loss to follow-up, and 7) threats to external validity. Conclusions: Economic claims made by the authors of a number of trial-based economic evaluations have generally been favorable to second-generation antipsychotics. However, the methodological issues the authors of the current study identified suggest that there is no clear evidence that atypical antipsychotics generate cost savings or are cost-effective in general use among all schizophrenia patients. Psychiatrists, researchers, and administrators should consider the methodological issues highlighted in interpreting study results. These issues should be addressed in future trial designs.
Antipsychotic medications make up one of the fastest growing segments of the rapidly growing pharmaceutical sector. The growth is primarily a result of a shift from conventional or first-generation antipsychotics (chlorpromazine, haloperidol, phenothiazine, etc.) to newer second-generation antipsychotics (clozapine, olanzapine, risperidone, quetiapine, etc.). Because the newer second-generation antipsychotics are relatively more expensive than the first-generation antipsychotics, most of which are available generically, antipsychotic expenditures have increased several-fold over the last decade. For instance, Medicaid expenditures for antipsychotic medications increased from $484 million in 1995 to $3.73 billion in 2002 (1, 2) . Given limited health care resources, assessment of the value of the costs of second-generation antipsychotics relative to first-generation antipsychotics is critical for resource allocation decisions.
Cost-effectiveness analysis is one of the most common methods used in the medical literature to address such questions. This analysis explicitly expresses tradeoffs among treatment interventions by comparing differences in resources used (costs) and health benefits achieved (e.g., symptom reduction, function recovery, or quality-adjusted life-years). Cost-effectiveness analyses frequently are based on data from randomized clinical trials in which prospective economic information is collected along with clinical endpoints.
To identify published randomized clinical trial-based cost-effectiveness analyses for second-generation antipsychotics compared to first-generation antipsychotics, we conducted a MEDLINE literature search from 1985 to 2003 using terms related to schizophrenia treatment (e.g., “schizophrenia” or “antipsychotic[s]”), costs (e.g., “cost[s],” “cost-effectiveness,” or “economic[s]”), and clinical trials (e.g. “trial[s]” or “randomi[s or z]ed”) in the title, abstract, or MeSH heading. This search identified nine randomized clinical trial-based cost-effectiveness studies of antipsychotic medications from a total of seven trials (two pairs of studies each used data from a common trial but differed on the subgroups or endpoints analyzed). Eight of these studies compared clozapine (3 – 5), olanzapine (6 – 8), or risperidone (9) or both olanzapine and risperidone (10) with first-generation antipsychotics, mainly haloperidol. The ninth study (11) compared two second-generation antipsychotics and did not have a first-generation antipsychotic treatment arm; thus, it was excluded. Hence, our study included eight cost-effectiveness evaluations that were based on six clinical trials of second-generation antipsychotics versus first-generation antipsychotics.
A review of the abstracts for the included studies indicated that six of the eight explicitly reported that second-generation antipsychotics were cost-effective compared to first-generation antipsychotics (3, 5, 9) or reported findings that suggested that second-generation antipsychotics were cost-effective (e.g., more effective with similar costs or less costly with similar benefits) (4, 6, 7) . Although some of these six attempted to limit the populations for which the cost-effectiveness claims were being made (e.g., Rosenheck et al. [3] ) or added qualifications to the cost-effectiveness claims (e.g., Essock et al. [5] ), only two studies suggested that second-generation antipsychotics were unlikely to be cost-effective (8, 10) . In none of the eight abstracts was there a statement that first-generation antipsychotics were cost-effective compared to second-generation antipsychotics. Thus, the weight of the evidence appears to suggest that compared to first-generation antipsychotics, second-generation antipsychotics are a good value for their cost.
Although randomized clinical trials are considered to be the gold standard for comparing alternative medical therapies, random assignment does not in and of itself guarantee valid or reliable results. Without appropriate methods of measurement, the analysis, design, and economic evaluation with randomized clinical trials may be biased or imprecise or have limited applicability. This article reviews appropriate methods of measurement, analysis, and design of cost-effectiveness studies in randomized clinical trials and, in light of these methods, discusses the imprecision, bias, and limitations of the eight trial-based economic evaluations comparing second-generation antipsychotics to first-generation antipsychotics. The conclusions regarding the relative cost-effectiveness of second-generation antipsychotics compared to first-generation antipsychotics are then reconsidered. Our objective was not to evaluate each study on an exhaustive list of standards for cost-effectiveness analyses, such as those summarized in Gold et al. (12), but to identify the essential features that affect the validity of cost-effectiveness analysis in randomized clinical trials and appraise the current state of the trial-based cost-effectiveness literature on antipsychotic medications based on these features.
Measurement in Economic Evaluation of Randomized Clinical Trials
Issue 1. Measurement of Costs
The costs that are most appropriate for inclusion in an analysis depend on its “perspective.” The term “perspective,” when used in economic analyses, refers to whose costs are counted and, thus, to what is quantified. For instance, an analysis from the insurer’s perspective would include payments to providers but not out-of-pocket payments by patients. The most comprehensive perspective is that of society, which includes all costs but not necessarily all financial transactions, on all levels attributable to an illness’s impact and treatment.
For some decision makers, direct health care costs, such as the cost of drugs, hospitalization, and health care personnel, are of greatest interest (12) (pp. 179–181). For others, direct non-health-care costs, such as the time family members spend providing home care and costs of transportation to and from clinics, are also of interest. To better serve the broadest set of decision makers and to aid in the comparison of multiple studies, analysts should evaluate a therapy’s effect on both direct health care costs and direct non-health-care costs from a societal perspective. In addition, evaluation of indirect costs, such as productivity costs and patient time costs, including travel and waiting time as well as time spent receiving treatment, has the added advantage that it can be used to evaluate claims that newer drugs may help patients lead more productive lives. However, productivity costs may be correlated with health-related quality of life. If the effectiveness component of the cost-effectiveness ratio assesses health-related quality of life, then productivity costs should be presented separately to avoid double counting (12) . Optimally, studies should include more than one perspective because differing perspectives can illustrate the often-competing interests of various stakeholders, as well as barriers that may threaten implementation of treatments that are beneficial to society but may be costly for some stakeholders.
Three of the eight studies included both health care and non-health-care costs (3 – 5) . Four studies evaluated direct health care costs alone (6 – 8, 10) . One study quantified drug acquisition costs only (9), but for most decision makers, this approach is too narrow because costs that are not immediate to the intervention can be affected by it. In the three studies that assessed non-health-care costs, they made up a relatively small proportion of total costs and contributed little to the differences in costs between treatments in these studies. This surprising result was likely related to the relatively short time frames of the analyses and the fact that not all types of non-health-care costs were accounted for in these studies.
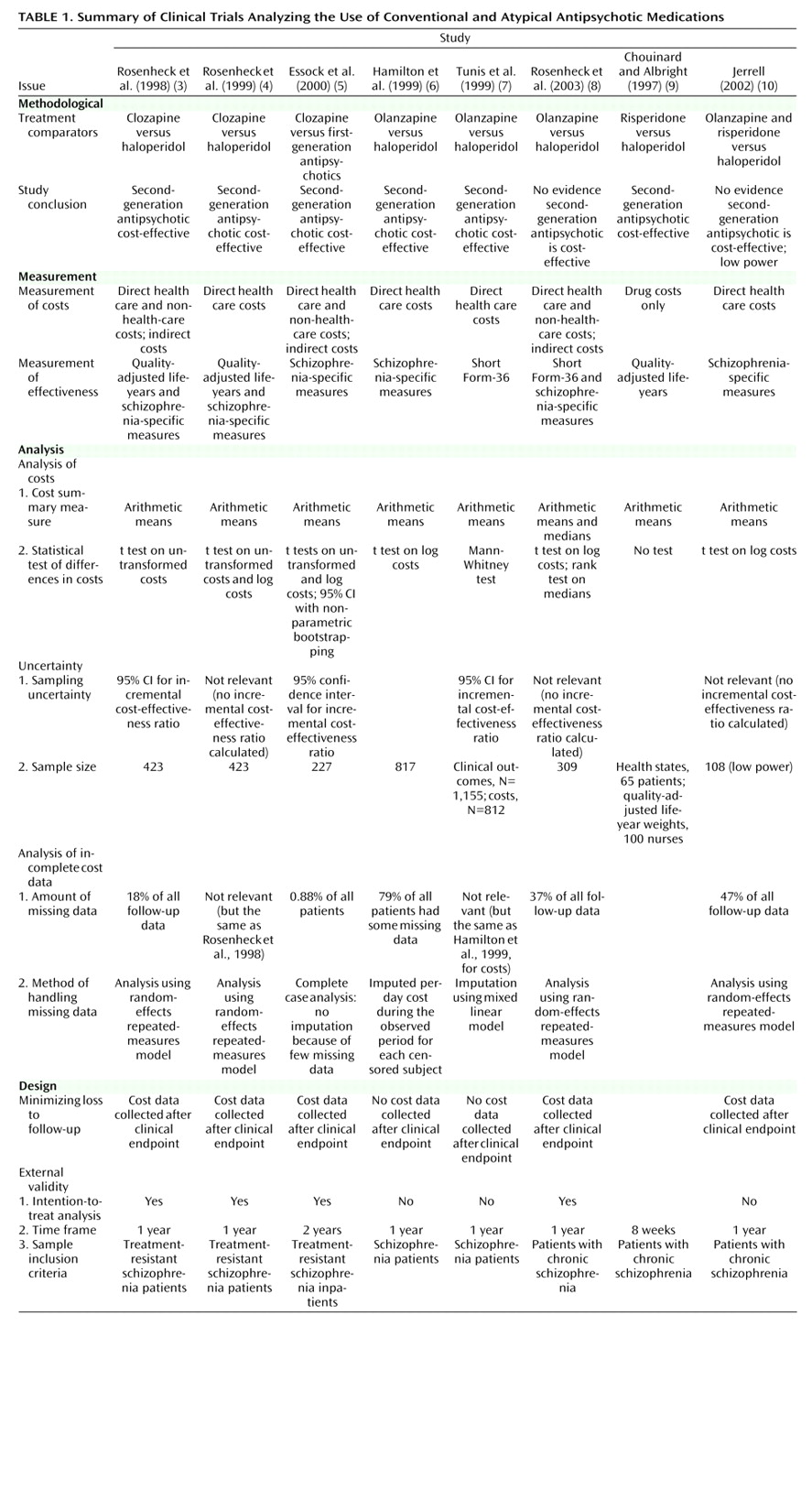
A summary of the eight trial-based economic evaluations of second-generation antipsychotics versus first-generation antipsychotics is presented in Table 1 .
Issue 2. Measurement of Effectiveness
Ideally, analysts adopt a single outcome for use in economic evaluations 1) that allows direct comparison of therapies across a number of domains, 2) that allows comparison across therapeutic areas and illnesses, and 3) for which one generally understands how much one is willing to pay to buy a unit of this outcome. In most areas of health technology assessment, this outcome is the quality-adjusted life-year (12) . Quality-adjusted life-years incorporate length of survival and its quality into a single measure. Values generally range between 0 (death) and 1 (perfect health) (e.g., a health state with a utility value of 0.8 indicates that a year in that state is worth 0.8 of a year with perfect health), although there can be states worse than death (i.e., less than 0) that are conceivably not uncommon in mental disorders (e.g., suicide).
Three studies used quality-adjusted life-years as an effectiveness measure in their evaluations (3, 4, 9) . One potential reason for the limited use of quality-adjusted life-years is that currently available instruments appear to focus on problems such as physical pain and motor functioning rather than on domains of health that are affected by psychotic illnesses (3) and thus may not be sensitive to disease-specific changes in function (13) . In addition, some consider individuals with chronic schizophrenia unable to provide valid and reliable measures of quality-adjusted life-years (9) . Systematic reviews of the reliability and validity of the general preference instruments, such as the Quality of Well-Being instrument (14 – 16) and the EuroQoL-5D (17) that have been used to assess quality-adjusted life-years in psychotic and other serious mental disorders, do not support these claims. Most suggest that quality-adjusted life-year scores correlate either cross-sectionally with disease severity or longitudinally with changes in disease severity. That may be because for most of the instruments, the subjects reported their current level of functioning, whereas the quality-adjusted life-year score is calculated by use of a scoring rule that has been constructed from responses made by the general public. However, additional research is needed to determine whether quality-adjusted life-year calculations with existing scoring instruments are adequate to assess quality of life in populations in which suicidality is frequent.
The five studies that did not use quality-adjusted life-years as an outcome used a wide variety of alternative outcome measures, including those based on the Brief Psychiatric Rating Scale score (6), Positive and Negative Syndrome Scale (PANSS) total scores (8), and Short Form-36 Physical and Mental Health component scores (7) . One study (10) used 12 mental health and satisfaction measures, whereas another (5) used four measures of effectiveness, namely, extrapyramidal symptom-free months, measures of disruptiveness and psychiatric symptoms, and weight gain. In addition to the quality-adjusted life-year measure, two of the studies by Rosenheck et al. (3, 4) used a composite health index for schizophrenia. The difficulty in comparing results among these measures and our limited understanding of the willingness to pay for observed changes in these measures reinforces the need to develop more uniform and interpretable measures of effectiveness.
Analysis in Economic Evaluation in Randomized Clinical Trials
Issue 3. Analysis of Costs
Cost-effectiveness (and cost-benefit) analysis should be based on differences in the arithmetic mean of costs and the arithmetic mean of effects between available treatment options (18) . One should report these means and their difference, measures of variability and precision, and an indication of whether or not the observed differences in the arithmetic mean are likely to occur by chance. In addition, the reporting of medians and other percentiles of the distribution are useful in describing costs.
Evaluation of the differences in arithmetic mean costs and the determination of the likelihood that they are due to chance is complicated by the fact that health care costs are typically characterized by highly skewed distributions, with long and sometimes awkwardly heavy right tails (19) . The existence of cost distributions with long, heavy tails has led some observers to reject the use of arithmetic means and the common statistical methods used for their analysis, such as t tests of means and linear regression, because they are sensitive to the heaviness of the tail. For example, some investigators prefer to evaluate the natural log costs, which may or may not be more normally distributed than costs. Others have adopted nonparametric tests of the median of costs, for example, for univariate tests, for the Mann-Whitney test, and for multivariable tests and median regression. However, statistical inferences about these other statistics need not be representative of inferences about the arithmetic mean. The use of tests of statistics other than the arithmetic mean also divorces inference from estimation. For example, use of a multivariable model to predict the log costs yields inferences about the difference in log costs and does not provide a direct estimate of the predicted difference in costs. More recently, the use of the generalized linear model in cost estimation has been proposed as a method of overcoming many of the shortcomings of ordinary least squares models of costs and log costs (20 – 22) . In addition, given the multiple problems confronting analysis of costs, it is optimal to perform both univariate and multivariable tests of difference in the mean of costs or to use methods proposed for the selection of an appropriate multivariable model (20) .
All eight studies reported measures of mean costs in the comparison groups. Rosenheck et al. (8) also reported median costs. However, they demonstrated little agreement in their approach to the statistical analysis of the differences in costs. Three studies performed statistical tests of arithmetic mean costs. Two of the studies by Rosenheck et al. (3, 4) reported t tests of untransformed costs, and Essock et al. (5) performed a nonparametric bootstrap test to derive 95% confidence intervals (CIs) around the cost difference, in addition to performing t tests on untransformed and transformed costs.
The remaining five studies analyzed something other than the arithmetic mean. For example, three studies (6, 8, 10) conducted t tests on the logarithmic transformation of costs (Hamilton et al. [6], with multiple analyses of variance, Rosenheck et al. [8] and Jerrell [10], with analysis of covariance of logarithms). None of these authors adequately addressed the problems posed by retransformation from the log of cost scale back to the original cost scale. Rosenheck et al. (8) and Tunis et al. (7) performed nonparametric rank sum tests or Mann-Whitney tests, which are usually interpreted as tests of medians. Finally, Chouinard and Albright (9) derived their cost estimate by comparing published drug acquisition prices (i.e., they were not measured at the patient level), and thus no statistical test was used to determine whether the predicted difference was statistically significant.
Issue 4. Uncertainty
Sampling Uncertainty
Economic outcomes observed in randomized clinical trials are the result of samples drawn from the population. Thus, all studies should report the uncertainty in these outcomes that results from such sampling. Common measures of this uncertainty are CIs for either the cost-effectiveness ratio or the estimate of net monetary benefit (a transformation of the cost-effectiveness ratio calculated by first multiplying the outcome measure by a cost-effectiveness ratio representing one’s willingness to pay for the outcome and, second, by subtracting out costs).
Only three of the eight studies reported CIs for cost-effectiveness ratios (3, 5, 7) . In all three, the point estimates indicated that compared to first-generation antipsychotics, second-generation antipsychotics have acceptable cost-effectiveness ratios, but the CIs contained cost-effectiveness ratios that, depending upon one’s maximum willingness to pay, may be unacceptably high (i.e., not cost-effective). Thus, in none of the three studies could we be 95% confident that second-generation antipsychotics represent good value for the cost compared with haloperidol or other first-generation antipsychotics.
The remaining five studies failed to report on the stochastic uncertainty surrounding this comparison. Hamilton et al. (6) may not have reported CIs for the cost-effectiveness ratio because they found significant clinical improvements without any significant difference in costs (i.e., they presumed the result represented identification of a dominant strategy). But the three studies that reported CIs (3, 5, 7) also had point estimates that indicated apparent dominance of one therapy over another; however, their CIs suggested that they did not have sufficient statistical power to allow one to confidently conclude that one had observed such dominance. Jerrell (10) and Rosenheck et al. (8), on the other hand, may not have reported such an interval because no differences were observed for either costs or clinical outcomes. In fact, Jerrell (10) stressed that her study was underpowered. However, estimation of a CI for the cost-effectiveness ratio would still have been useful in all five studies.
Power and Sample Size
When designing randomized clinical trial-based economic studies, investigators should perform power calculations for the cost-effectiveness endpoint so that one can understand whether a statistically insignificant result may be due to a lack of power (23, 24) . Several of the studies that we evaluated reported results for outcomes for which they appeared underpowered. The sample sizes across the nine studies varied from 65 in Chouinard and Albright (9) to 817 in Hamilton et al. (6) . Although Chouinard and Albright (9) reported their sample size as 130, the utility value (i.e., the effectiveness measure) was assigned to a total of 65 patients in three drug treatment groups. Hence, although many studies evaluated in this article reported large differences in costs or effects between different antipsychotic agents, the lack of statistical significance of these results might, as indicated by Jerrell (10) about the author’s own results, be due to these studies being underpowered.
Issue 5. Analysis of Incomplete Cost Data
Psychiatric randomized clinical trials that follow participants for clinically meaningful lengths of time are prone to high dropout rates. When data are missing, studies should explicitly report the amount of missing data and whether or not there was an indication that the data appeared to be missing at random. They should also adopt appropriate statistical methods to address the problems posed by missing data (25 – 27) . If these problems are not appropriately addressed, estimates of the treatment effect will be biased (28) . Recent interest in the issue of censored cost data has led to the proposal of several analytic methods for addressing loss to follow-up. Lin (25) presented a method that appropriately adjusts for censoring under restrictive assumptions, and methods involving inverse-probability weighting, which require weaker assumptions, have also been proposed (26, 27) . O’Hagan and Stevens (29) recommended that these methods be used because naive estimation can lead to serious bias.
Five of the eight studies explicitly reported the amounts of missing data (3, 5, 6, 8, 10) . Rosenheck et al. (4) and Tunis et al. (7) did not report the amount of missing data, but given that they used data from trials for which these data were reported (3, 6), one can infer the amount of missing data. Chouinard and Albright (9), on the other hand, never explicitly mentioned whether or not there was any missing data.
Essock et al. (5) had so little missing data that they could safely ignore it. However, in a number of studies, there were large amounts of missing data. For example, Rosenheck et al. (8) reported that 37% of all follow-up data were missing, whereas Jerrell (10) reported that 47% of all follow-up data were missing. Termination of follow-up/withdrawal over the 1-year time frame of the analysis was 83% in the studies by Hamilton et al. (6) and Tunis et al. (7) . For these two studies, data were unavailable after withdrawal from the randomized clinical trial.
Four studies (3, 4, 8, 10) used a random-effects repeated-measures model for their analyses. This type of model allows for the inclusion of available data from individuals who eventually drop out of the randomized clinical trial. Tunis et al. (7) imputed missing values by use of a mixed linear model. The underlying assumption of all of these approaches to addressing missing data are that the costs for subjects during the period when they are not observed can be represented by the adjusted means of the subjects who are observed during the period. Although this method will result in an unbiased result if the reasons for being missing are unlikely to be correlated with the outcome (referred to as being missing completely at random [30] ), the inverse probability methods of Lin (26) and Bang and Tsiatis (27) offer several advantages by incorporating information related to the probability of being censored.
Hamilton et al. (6) imputed missing values by use of a per-day cost during the period observed for each censored subject. This method assumes both that costs are missing completely at random and that costs are homogenous over time. Neither of these assumptions may be warranted, given that one of the primary reasons for missing data in this study was lack of response. This violation suggests that these authors, and Tunis et al. (7), may have adopted biased methods for addressing the large amounts of missing data in their studies.
Design in Economic Evaluation in Randomized Clinical Trials
Issue 6. Minimizing Loss to Follow-Up
Although one should adopt analytic approaches to address missing data that arise during the study, ideally, one should design studies in such a way that they minimize the occurrence of such missing data. For example, study designs should include plans to aggressively pursue subjects and data throughout the trial. One long-term study of the treatment of bipolar disorder (31) was designed from the outset to respond to missed interviews by 1) intensive outreach to reschedule the assessment, 2) then telephone assessment, 3) then interviews of a proxy who had been identified and consented to at the time of random assignment. Psychiatric randomized clinical trials should also ensure that follow-up continues until the end of the study period and that data collection should not be discontinued simply because a subject reaches a clinical or treatment stage, such as failure to respond. This last recommendation may conflict with some commonly used efficacy designs that are event driven and end follow-up when a participant reaches such a stage. However, the economic impact of these outcomes or events can only be measured if patients are followed beyond the time when they occur.
Five of the eight studies were based on trials that reported explicit strategies for minimizing missing cost data. The three studies by Rosenheck et al. (3, 4, 8), Essock et al. (5), and Jerrell (10) continued to collect cost data for participants independent of the observed clinical outcome (e.g., treatment failure or switching of therapy). Chouinard and Albright (9) did not indicate what they did or did not do to prevent missing data. The trial on which the Hamilton et al. (6) and Tunis et al. (7) studies were based, on the other hand, used a design that consciously created missing data. In this trial, 40% of the participants dropped out of the study during its 6-week acute phase (32) . Then all data collection was intentionally discontinued for the patients who did not meet a predefined level of treatment response, whereas the remainder were eligible to continue the study for a 46-week maintenance phase.
Issue 7. External Validity
Frequently, the priority of the design of randomized clinical trials of psychopharmacological agents is to generate an internally valid measure of the efficacy of treatment (31) . Given that the primary purpose of cost-effectiveness analysis is to inform real-world decision makers about how to respond to real-world health care needs, the design of cost-effectiveness studies should, in addition, consider issues of external validity. This difference in emphasis is similar to the one that has been noted between efficacy and effectiveness studies (31, 33) . In this section, we addressed methods of randomized clinical trial design that specifically relate to maximizing the usefulness of cost-effectiveness analysis from clinical trials.
Intention-to-Treat Analysis
Given that in real-world settings, economic questions relate to treatment decisions (e.g., whether to prescribe a second-generation antipsychotic), not whether the patient received the drug prescribed or whether, once he or she started the prescribed drug, the individual was switched to other drugs, the costs and benefits associated with these later decisions should be attributed to the initial treatment decision. Thus, cost-effectiveness analyses in randomized clinical trials should adopt an intention-to-treat design.
All three of the reports by Rosenheck et al. (3, 4, 8) used intention-to-treat analyses, as did Essock et al. (5) . In the randomized clinical trial that compared clozapine and haloperidol (3), 40% of the patients who initiated therapy with clozapine eventually were unblinded, discontinued their use of the study medication, and then crossed over to a standard antipsychotic medication (including haloperidol). Of those initiating therapy with haloperidol, 72% eventually were unblinded, discontinued their use of the study medication, and then crossed over to other antipsychotic medications (22% received clozapine treatment). Thus, all three of the intention-to-treat cost-effectiveness analyses captured some of the issues that confront clinicians when making choices in the real world.
On the other hand, the large numbers of patients who did not continue in the study after learning of their randomization assignment may mean that the analysis by Jerrell (10) could not follow the principles of intention-to-treat, and the intentional discontinuation of nonresponders and those who switched treatment regimens in the studies by Hamilton et al. (6) and Tunis et al. (7) suggests that theirs were not intention-to-treat analyses. Finally, as with many of the issues related to missing data, Chouinard and Albright (9) provided no information with which to judge whether they conducted an intention-to-treat analysis.
Time Frame
Randomized controlled trials of long-term treatments are time limited, whereas treatment for chronic conditions is not. If long-term use yields outcomes that generally cannot be observed by the use of shorter time frames or if the cost-effectiveness ratio is heterogeneous with the time of follow-up, making therapeutic decisions based solely on results observed within short-term randomized clinical trials may be inappropriate. For example, the longest follow-up among the eight studies was 2 years (5), whereas most had follow-ups of 1 year or less. However, there is growing observational evidence suggesting that atypical antipsychotics are associated with long-term complications, such as diabetes and cardiovascular disease (34) . Except for the onset of weight gain, addressed, for example, by Rosenheck et al. (8), none of the currently evaluated studies took these longer-term outcomes into account. One approach to addressing these limitations is with decision analysis. However, currently published decision models in schizophrenia, whose time frames range from 1 to 5 years, do not project outcomes long enough to incorporate such long-term effects (35) .
Sample Inclusion Criteria
Many phase III efficacy trials and some effectiveness trials may employ study samples that do not resemble the more heterogeneous population found in general practice that decision makers must consider when making resource allocation decisions. The three studies comparing clozapine with haloperidol, for example, were limited to schizophrenia patients with both treatment resistance and high inpatient use. The efficacy of first-generation antipsychotics and second-generation antipsychotics may be different in such patients compared to the general schizophrenic population. Hence, the results of these studies may not be generalizable to the 80%–90% of non-treatment-resistant schizophrenia patients (36) . In addition, Rosenheck et al. (4) found that among this already narrow population, clozapine was cost-effective only among those with high levels of hospital use.
In actual clinical practice, antipsychotics may be used for indications for which no economic evidence of value for the cost exists. For example, it has been reported that among patients in the VA system who were given prescriptions for second-generation antipsychotics, 43% were for the treatment of psychiatric illnesses other than schizophrenia or schizoaffective disorder (37) . In addition, most of the subjects had few inpatient days, which, based on cost-effectiveness findings from Rosenheck et al. (4), suggests that therapy may not result in cost savings for the health care system. Rosenheck et al. (37) made a convincing argument that cost-effectiveness in medication use in actual practice and alternative strategies for the use of second-generation antipsychotics in a health care system should be analyzed.
Validity of the Conclusions of Economic Evaluations of Antipsychotic Drugs
Clozapine Versus First-Generation Antipsychotics
The three studies that compared clozapine with first-generation antipsychotics generally concluded that for treatment-resistant patients with high hospital use, clozapine had lower costs and better outcomes over some effectiveness domains (3 – 5) . Generally, these studies were well designed, but none reported a statistically significant difference in costs between treatment groups (issue 3), and one study reported a 95% CI for the cost-effectiveness result only among the small subset of patients with the highest levels of inpatient service use (issue 4). However, given that the samples in these studies were limited to schizophrenia patients with both treatment resistance and at least 30 days of hospitalization, their results are unlikely to be applicable to the 80%–90% of non-treatment-resistant schizophrenia patients (issue 7) (36) .
Olanzapine Versus First-Generation Antipsychotics
Of the three studies that compared olanzapine with haloperidol, two found that olanzapine reduced costs and improved the quality of life compared to haloperidol (6, 7) . Both studies were based on the same randomized clinical trial, which discontinued patients who either failed to respond by week 6 or changed their treatment regimen (issues 5 and 6). As a result, less than 17% of those who were randomly assigned were still in the study by the end of the first year. This extreme loss of data, coupled with the fact that the reason for dropouts was associated with treatment effectiveness, in which case the costs and outcomes of the patients after they switched drugs or failed to respond are unlikely to be represented by the costs and outcomes observed among patients while they participated in the trial, suggests that the 1-year cost-effectiveness results of these two studies may be severely biased (issue 5). On the other hand, the study by Rosenheck et al. (8), which found no significant advantages in the effectiveness of olanzapine and higher costs when compared with haloperidol, was based on a trial that followed both treatment nonresponders and those who changed their treatment regimen. In this study, 59% of the subjects remained in the trial by the end of the first year.
Risperidone Versus First-Generation Antipsychotics
Two studies compared risperidone with first-generation antipsychotics (9, 10) . The favorable cost-effectiveness ratio for risperidone in the study by Chouinard and Albright (9) was based on a comparison of 22 risperidone patients and 21 haloperidol patients followed for 8 weeks. Although the study did not report a statistical test (issue 3), this small sample should lead to a lack of statistical significance for their comparative findings (issue 4). Furthermore, this study included drug-acquisition costs alone and did not account for other health care or non-health-care costs that may be affected by the intervention (issue 1). The second study, by Jerrell (10), comparing risperidone and olanzapine with first-generation antipsychotics found both second-generation antipsychotics to have no advantages in outcomes but higher mental health treatment costs than first-generation antipsychotics. However, this conclusion was limited by small sample sizes and large loss to follow-up (issues 4 and 5).
Conclusions
Economic claims made by the authors of a number of randomized clinical trial-based economic evaluations have generally—but not unanimously—been favorable for second-generation antipsychotics over first-generation antipsychotics. However, the methodological problems we have identified raise questions as to the quality of the evidence behind those claims. Our critical review suggests that currently there is no clear evidence that atypical antipsychotics generate cost savings or are cost-effective in general use among all schizophrenia patients.
Methodological problems, such as the ones we documented, are not limited to the antipsychotic literature alone but instead have been found to persist in most randomized clinical trial-based economic evaluations in all areas of medicine. Systematic review by Barber and Thompson (38) and Doshi et al. (39) of the analysis and interpretation of cost data from all published trials in 1995 (38) and in 2003 (39), which covered a wide variety of clinical areas, including cancer, heart disease, nursing, and psychiatry, revealed a lack of statistical awareness and frequent reporting of potentially misleading conclusions in the absence of supporting statistical evidence. However, in light of the exponential growth in atypical antipsychotic expenditures over the last few years, the poor quality of the economic evidence supporting the value of second-generation antipsychotics over first-generation antipsychotics takes on added significance. Clinicians, administrators, insurers, and other stakeholders should recognize that there is a need for comprehensive phase IV studies that compare second-generation antipsychotics to first-generation antipsychotics. The goal of these studies should be to determine whether there are more cost-effective treatment strategies than current standard care and thus provide optimal input into future decision-making processes.
Some of the limitations in methods may be due to the fact that most of the advances in design and statistical techniques for the analysis of cost and cost-effectiveness are published in highly technical economics or biostatistical journals. Recently, there have been several attempts to make them available to a broader audience (40, 41) . Improved economic evidence may lead to cost-effectiveness data playing a greater role in insurance coverage and formulary decisions surrounding antipsychotics. Also, consistent and reliable economic evidence from improved cost-effectiveness analysis methods will influence resource allocation decisions toward welfare maximization. Future randomized clinical trial-based economic evaluations of current second-generation antipsychotics versus first-generation antipsychotics, of newer antipsychotic agents, and of other psychotropic therapies should attempt to address the priority issues identified here to enhance the validity of their findings and ensure their usefulness to decision makers.
Footnote
Presented in part at the second NIMH Pharmacoeconomic Research Directions Workshop, Washington, D.C., May 24, 2004. Received Aug. 20, 2004; revision received March 19, 2005; accepted May 13, 2005. From the Division of General Internal Medicine, University of Pennsylvania, Philadelphia; the Leonard Davis Institute of Health Economics, Philadelphia; the Providence VA Medical Center, Providence; and the Department of Psychiatry and Human Behavior, Brown University, Providence. All authors report no competing interests. Address correspondence and reprint requests to Dr. Polsky, Blockley Hall, Rm. 1212, 423 Guardian Dr., Philadelphia 19104; [email protected] (e-mail).Supported by a National Institute of Alcoholism and Alcohol Abuse grant (R01-AA-12664-01) and by VA Cooperative Study 430, “Reducing the Efficacy-Effectiveness Gap for Bipolar Disorder.”The authors thank Anirban Basu for his review and comments on the article.
References
1.
Group L: Access and Utilization of New Antidepressant and Antipsychotic Medications: Report Submitted to the Office of the Assistant Secretary for Planning and Evaluation and the National Institute of Mental Health, US Department of Health and Human Services. Rockville, Md, NIMH, 2000
Rosenheck R, Cramer J, Xu W, Grabowski J, Douyon R, Thomas J, Henderson W, Charney D (Department of Veterans Affairs Cooperative Study Group on Clozapine in Refractory Schizophrenia): Multiple outcome assessment in a study of the cost-effectiveness of clozapine in the treatment of refractory schizophrenia. Health Serv Res 1998; 33(part 1):1237–1261
Rosenheck R, Cramer J, Allan E, Erdos J, Frisman LK, Xu W, Thomas J, Henderson W, Charney D (Department of Veterans Affairs Cooperative Study Group on Clozapine in Refractory Schizophrenia): Cost-effectiveness of clozapine in patients with high and low levels of hospital use. Arch Gen Psychiatry 1999; 56:565–572
Essock SM, Frisman LK, Covell NH, Hargreaves WA: Cost-effectiveness of clozapine compared with conventional antipsychotic medication for patients in state hospitals. Arch Gen Psychiatry 2000; 57:987–994
Hamilton SH, Revicki DA, Edgell ET, Genduso LA, Tollefson G: Clinical and economic outcomes of olanzapine compared with haloperidol for schizophrenia: results from a randomised clinical trial. Pharmacoeconomics 1999; 15:469–480
Tunis SL, Johnstone BM, Gibson PJ, Loosbrock DL, Dulisse BK: Changes in perceived health and functioning as a cost-effectiveness measure for olanzapine versus haloperidol treatment of schizophrenia. J Clin Psychiatry 1999; 60(suppl 19):38–45
Chouinard G, Albright PS: Economic and health state utility determinations for schizophrenic patients treated with risperidone or haloperidol. J Clin Psychopharmacol 1997; 17:298–307
Edgell ET, Andersen SW, Johnstone BM, Dulisse B, Revicki D, Breier A: Olanzapine versus risperidone: a prospective comparison of clinical and economic outcomes in schizophrenia. Pharmacoeconomics 2000; 18:567–579
Pyne JM, Sullivan G, Kaplan R, Williams DK: Comparing the sensitivity of generic effectiveness measures with symptom improvement in persons with schizophrenia. Med Care 2003; 41:208–217
Patterson TL, Kaplan RM, Grant I, Semple SJ, Moscona S, Koch WL, Harris MJ, Jeste DV: Quality of well-being in late-life psychosis. Psychiatry Res 1996; 63:169–181
Montes JM, Ciudad A, Gascon J, Gomez JC: Safety, effectiveness, and quality of life of olanzapine in first-episode schizophrenia: a naturalistic study. Prog Neuropsychopharmacol Biol Psychiatry 2003; 27:667–674
Prieto L, Novick D, Sacristan JA, Edgell ET, Alonso J: A Rasch model analysis to test the cross-cultural validity of the EuroQoL-5D in the schizophrenia outpatient health outcomes study. Acta Psychiatr Scand Suppl 2003; 416:24–29
Willan AR: Analysis, sample size, and power for estimating incremental net health benefit from clinical trial data. Control Clin Trials 2001; 22:228–237
Bauer MS, Williford WO, Dawson EE, Akiskal HS, Altshuler L, Fye C, Gelenberg A, Glick H, Kinosian B, Sajatovic M: Principles of effectiveness trials and their implementation in VA cooperative study 430: reducing the efficacy-effectiveness gap in bipolar disorder. J Affect Disord 2001; 67:61–78
Tollefson GD, Beasley CM Jr, Tran PV, Street JS, Krueger JA, Tamura RN, Graffeo KA, Thieme ME: Olanzapine versus haloperidol in the treatment of schizophrenia and schizoaffective and schizophreniform disorders: results of an international collaborative trial. Am J Psychiatry 1997; 154:457–465
Basu A: Cost-effectiveness analysis of pharmacological treatments in schizophrenia: critical review of results and methodological issues. Schizophr Res 2004; 71:445–462
Rosenheck R, Leslie D, Sernyak M: From clinical trials to real-world practice: use of atypical antipsychotic medication nationally in the department of veterans affairs. Med Care 2001; 39:302–308
Doshi JA, Glick HA, Polsky D: Analyses of cost data in economic evaluations conducted alongside randomized controlled trials. Value Health 2006; 9:334–340
Ramsey S, Willke R, Briggs A, Brown R, Buxton M, Chawla A, Cook J, Glick H, Liljas B, Petitti D, Reed S:Good research practices for cost-effectiveness analysis alongside clinical trials: the ISPOR RCT-CEA Task Force report. Value Health 2005; 8:521–533
If you have the appropriate software installed, you can download article citation data to the citation manager of your choice. Simply select your manager software from the list below and click Download.
For more information or tips please see 'Downloading to a citation manager' in the Help menu.
PsychiatryOnline subscription options offer access to the DSM-5-TR® library, books, journals, CME, and patient resources. This all-in-one virtual library provides psychiatrists and mental health professionals with key resources for diagnosis, treatment, research, and professional development.
Need more help? PsychiatryOnline Customer Service may be reached by emailing [email protected] or by calling 800-368-5777 (in the U.S.) or 703-907-7322 (outside the U.S.).
If the address matches an existing account you will receive an email with instructions to retrieve your username
Create a new account
Change Password
Password Changed Successfully
Your password has been changed
Login
Reset password
Can't sign in? Forgot your password?
Enter your email address below and we will send you the reset instructions
If the address matches an existing account you will receive an email with instructions to reset your password.
Change Password
Congrats!
Your Phone has been verified
×
As described within the American Psychiatric Association (APA)'s Privacy Policy and Terms of Use, this website utilizes cookies, including for the purpose of offering an optimal online experience and services tailored to your preferences. Please read the entire Privacy Policy and Terms of Use. By closing this message, browsing this website, continuing the navigation, or otherwise continuing to use the APA's websites, you confirm that you understand and accept the terms of the Privacy Policy and Terms of Use, including the utilization of cookies.
