Human genetics has sparked a revolution in medical science on the basis of the seemingly improbable notion that one can systematically discover the genes causing inherited diseases without any prior biological clue as to how they function. The method of genetic mapping, by which one compares the inheritance pattern of a trait with the inheritance patterns of chromosomal regions, allows one to find where a gene is without knowing what it is. The approach is completely generic, being equally applicable to spongiform brain degeneration as to inflammatory bowel disease.
Human geneticists are now beginning to explore a new genetic frontier, driven by an inconvenient reality: Most traits of medical relevance do not follow simple Mendelian monogenic inheritance. Such “complex” traits include susceptibilities to heart disease, hypertension, diabetes, cancer, and infection. The genetic dissection of complex traits is attracting many investigators with the promise of shedding light on old problems and is spawning a variety of analytical methods. The emerging issues turn out to be relevant not just to medical genetics, but to fundamental studies of mammalian development and applied work in agricultural improvement. The field is still at an early stage, but it is ready to explode much as it has done in recent years with the analysis of simple traits. The purpose of this article is to synthesize the key challenges and methods, to highlight some enlightening examples, and to identify further needs.
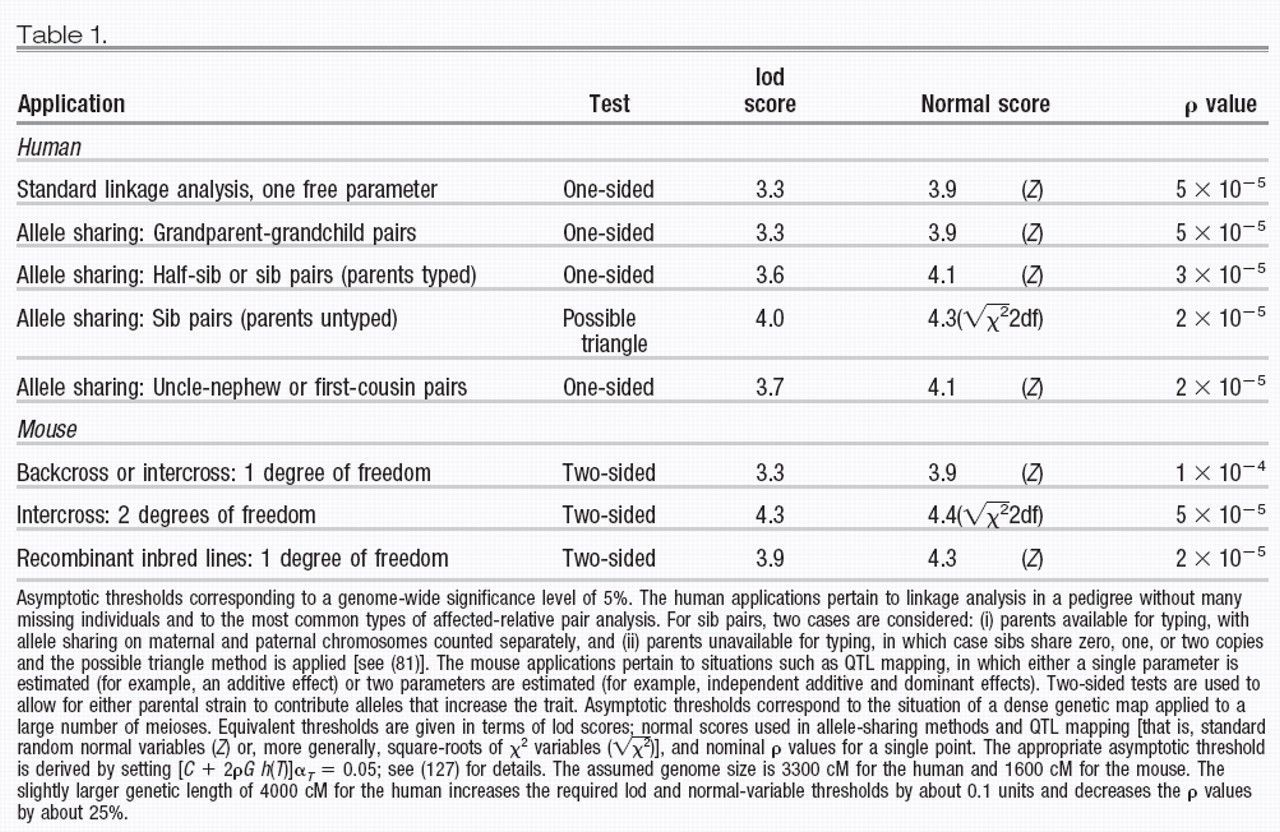
Linkage analysis
Linkage analysis involves proposing a model to explain the inheritance pattern of phenotypes and genotypes observed in a pedigree (Fig. 1). It is the method of choice for simple Mendelian traits because the allowable models are few and easily tested. However, applications to complex traits can be more problematic, because it may be hard to find a precise model that adequately explains the inheritance pattern.
Formally, linkage analysis consists of finding a model M
1, positing a specific location for a trait-causing gene, that is much more likely to have produced the observed data than a null hypothesis M
O, positing no linkage to a trait-causing gene in the region. The evidence for M
1 versus M
0 is measured by the likelihood ratio,
LR = Prob (Data|M
1)/Prob (Data|M
0), or, equivalently, by the lod score,
Z = log
10(
LR) (
49,
50).
The model M
1 is typically chosen from among a family of models M(Φ), where Φ is a parameter vector that might specify such information as the location of the trait-causing locus, the allele frequency at the trait and marker loci, the penetrance function, and the transmission frequencies from parent to child. Many of these parameters may already be known (such as penetrance functions from prior segregation analysis or marker allele frequencies from population surveys). The remaining, unknown parameters are chosen to be the maximum likelihood (ML) estimate, that is, the value Φ̂ that makes the data most likely to have occurred (
51). The null model M
0 corresponds to a specific null hypothesis about the parameters, Φ
0.
For example, the model for a simple Mendelian recessive or dominant disease is completely specified except for the recombination frequency θ between the disease gene and a marker; the null hypothesis of nonlinkage corresponds to θ = 50% recombination.
The ML model M(Φ̂) is accepted (compared with M
0) if the corresponding maximum lod score
Ẑ is large, that is, exceeds a critical threshold
T. Of course, a crucial issue is the appropriate significance threshold. The traditional lod score threshold has been 3.0 (
50,
52), although the appropriateness of this choice is discussed in the section on statistical significance.
Applications.
Linkage analysis is the current workhorse of human genetic mapping, having been applied to hundreds of simple monogenic traits. Linkage analysis has also been successfully applied to genetically heterogeneous traits in some cases. The simplest situation is when unequivocal linkage can be demonstrated in a single large pedigree (with
Ẑ ≫ 3), even though other families may show no linkage. This has been done for such diseases as adult polycystic kidney disease, early-onset Alzheimer’s disease, and psoriasis (
53). If linkage cannot be established on the basis of any single pedigree, one can ask whether a subset of the pedigrees collectively shows evidence of linkage. Of course, one cannot simply choose those families with positive lod scores and exclude those with negative lod scores, as such an ex post selection criterion will always produce a high positive lod score. Instead, one must explicitly allow for genetic heterogeneity within the linkage model (through the inclusion of an admixture parameter α specifying the proportion of linked families), although care is required because the resulting lod score has irregular statistical properties (
54). Alternatively, families can be selected on the basis of a priori considerations. An example of this approach is provided by the genetic mapping of a gene for early-onset breast cancer (
BRCA1) to chromosome 17q (
55). Families were added to the linkage analysis in order of their average age of onset, resulting in a lod score that rose steadily to a peak of
Ẑ = 6.0 with the inclusion of families with onset before age 47 and then fell with the addition of later-onset pedigrees. Notwithstanding these successes, many failed linkage studies may result from cryptic heterogeneity. It is always wise to try to redefine traits to make them more homogeneous.
Linkage analysis can also be applied when penetrance is unknown. One approach is to estimate the ML value of the penetrance ρ within the linkage analysis. A particular concern is to avoid incorrectly overestimating ρ, because this can lead to spurious evidence against linkage (caused by individuals who inherit a trait-causing allele but are unaffected). One can guard against this problem by performing an affecteds-only analysis, in which one records unaffected individuals as “phenotype unknown” or, equivalently, sets the penetrance artificially low (ρ ≈ 0). This approach was important in studies of both early-onset and late-onset Alzheimer’s disease (
25,
56). In the latter case, the lod score increased from 2.20 with an age-adjusted penetrance function to 4.38 with an affecteds-only analysis.
Some traits are so murky that it is unclear who should be considered affected. Psychiatric disorders fall into this category, and investigators have explored using various alternative diagnostic schemes within their analysis. For example, schizophrenia might be defined strictly to include only patients meeting the
Diagnostic and Statistical Manual of Mental Disorders (DSM) criteria or be defined more loosely to include patients with so-called schizoid personality disorders (
57). This approach is permissible in theory but requires great care in adjusting the significance level to offset the effect of multiple hypothesis testing.
Linkage analysis can also be extended to situations in which two or more genes play a role in the inheritance of a disease, simply by examining the inheritance pattern of pairs of regions. Such an approach has been dubbed simultaneous search (
21,
58,
59). It can be applied to the situation of a genetically heterogeneous trait or to an interaction between two loci. Multiple sclerosis in large Finnish kindreds has been reported to be linked to the inheritance of both HLA on chromosome 6 and the gene for myelin basic protein on chromosome 18, on the basis of such a two-locus analysis (
60).
Limitations.
Linkage analysis is subject to the same limitations as any model-based method. It can be very powerful, provided that one specifies the correct model (
61,
62). Use of the wrong model, however, can lead one to miss true linkages and sometimes to accept false linkages (
63,
64). In particular, exclusion mapping of regions can only demonstrate absence of a trait-causing locus fitting the particular model tested (
50,
52). Finally, testing many models requires the use of a higher significance level, which may decrease the power to detect a gene; this issue is discussed in the section on statistical significance. The more complex the trait, the harder it is in general to use linkage analysis (
65).
Computation.
Calculating the likelihood ratio can be horrendously complicated in some cases and requires computer programs (
66,
67). Elston and Stewart invented the first practical algorithm for calculating likelihoods (
68,
69), which was implemented by Ott in the first general-purpose linkage program LIPED (
70) and is also at the heart of the widely used LINKAGE package (
71). However, the algorithm is not a complete panacea. In its original form it does not easily accommodate environmental or polygenic covariation among family members, which form the basis of so-called “mixed models” (
67,
72) used widely in genetic epidemiology (
73). In addition, it can be extremely slow for analysis with many genetic markers or inbred families. Alternative exact algorithms have been developed for some applications (
74), including one that allows multipoint homozygosity mapping (
75), but these tend to be limited to smaller pedigrees. Likelihoods can also be estimated by simulation-based methods, such as the Gibb’s sampler and Monte Carlo Markov chains (
76). There remain many important computational challenges in linkage analysis.
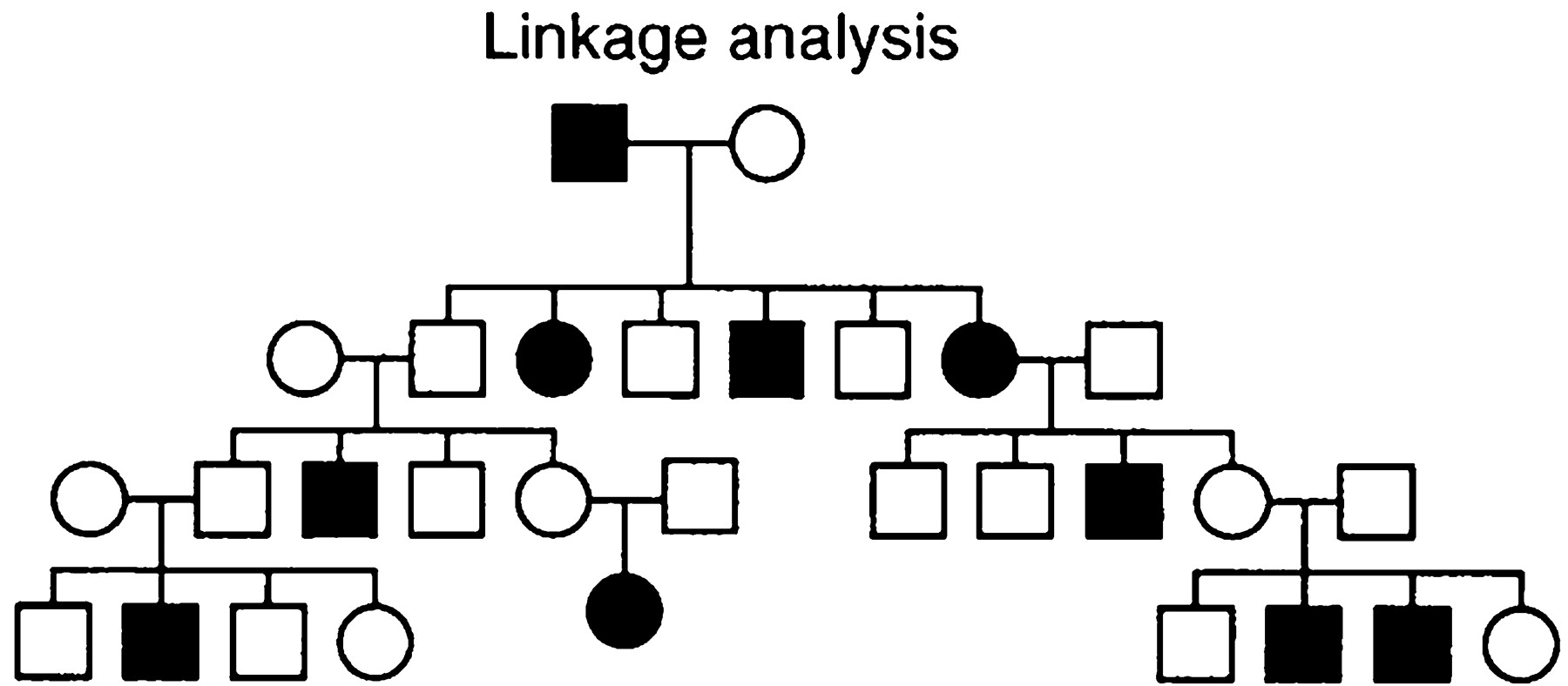
Allele-sharing methods
Allele-sharing methods are not based on constructing a model, but rather on rejecting a model. Specifically, one tries to prove that the inheritance pattern of a chromosomal region is not consistent with random Mendelian segregation by showing that affected relatives inherit identical copies of the region more often than expected by chance (Fig. 2). Because allele-sharing methods are nonparametric (that is, assume no model for the inheritance of the trait), they tend to be more robust than linkage analysis: affected relatives should show excess allele sharing even in the presence of incomplete penetrance, phenocopy, genetic heterogeneity, and high-frequency disease alleles. The tradeoff is that allele-sharing methods are often less powerful than a correctly specified linkage model.
Allele-sharing methods involve studying affected relatives in a pedigree to see how often a particular copy of a chromosomal region is shared identical-by-descent (IBD), that is, is inherited from a common ancestor within the pedigree. The frequency of IBD sharing at a locus can then be compared with random expectation. Formally, one can define an identity-by-descent affected pedigree-member (IBD-APM) statistic
where
xij(
s) is the number of copies shared IBD at position
s along a chromosome, and where the sum is taken over all distinct pairs (
i,
j) of affected relatives in a pedigree. The results from multiple families can be combined in a weighted sum
T(
s). Assuming random segregation,
T(
s) tends to a normal distribution with a mean μ and variance σ that can be calculated on the basis of the kinship coefficients of the relatives compared (
77,
78). Deviation from random segregation is detected when the statistic (
T − μ)/σ exceeds a critical threshold (see the section on statistical significance).
Sib pairs.
Affected sib pair analysis is the simplest form of this method. For example, two sibs can show IBD sharing for zero, one, or two copies of any locus (with a 25%–50%–25% distribution expected under random segregation). If both parents are available, the data can be partitioned into separate IBD sharing for the maternal and paternal chromosome (zero or one copy, with a 50%–50% distribution expected under random segregation). In either case, excess allele sharing can be measured with a simple χ
2 test (
79–
81).
Sib pair studies have played an important role in the study of type I diabetes. Excess allele sharing confirmed the important role of HLA, although the inheritance pattern fit neither a simple dominant or recessive model (
82,
83). With the availability of a comprehensive human genetic linkage map, sib pair analysis has been applied to a whole-genome scan, and excess allele sharing has been found at a locus on chromosome 11q, pointing to a previously unidentified causal factor in type I diabetes (
84). In a similar search restricted to the X chromosome, brothers concordant for the trait of homosexual orientation showed significant excess allele sharing (33 out of 40 cases) in the region Xq28, suggesting the involvement of a genetic factor influencing at least the particular subtype of homosexuality studied (
85). The same approach can be applied to affected uncle-nephew pairs and cousin pairs, for example.
IBD versus IBS.
One often cannot tell whether two relatives inherited a chromosomal region IBD, but only whether they have the same alleles at genetic markers in the region, that is, are identical by state (IBS). It is usually safe to infer IBD from IBS when a dense collection of highly polymorphic markers has been examined, but the early stages of genetic analysis may involve sparser maps with less informative markers. Two approaches have been developed to cope with this important practical difficulty. The first amounts to inferring IBD sharing on the basis of the marker data (expected IBD-APM methods) (
86), whereas the second uses another statistic based explicitly on IBS sharing (IBS-APM method) (
78,
87). (The inventors of the latter method dubbed it simply the APM method, but we prefer the more descriptive names used here.) Both approaches are important, although key statistical and computational issues remain open for each.
A number of recent studies have applied IBS-APM methods to complex traits. The angiotensinogen gene has been shown with IBS-APM analysis to be linked to essential hypertension in multiplex families, although the gene explains only a minority of the phenotype (
88). Similarly, linkage of late-onset Alzheimer’s disease to chromosome 19 could be established by IBS-APM, even though traditional lod score analysis gave more equivocal results (
25).
Quantitative traits.
Allele-sharing methods can also be applied to quantitative traits. An approach proposed by Haseman and Elston (
89) is based on the notion that the phenotypic similarity between two relatives should be correlated with the number of alleles shared at a trait-causing locus. Formally, one performs regression analysis of the squared difference Δ
2 in a trait between two relatives and the number
x of alleles shared IBD at a locus. The approach can be suitably generalized to other relatives (
90) and multivariate phenotypes (
91). It has been used, for example, to relate serum IgE levels with allele sharing in the region of the gene encoding interleukin-4 and bone density in postmenopausal women with allele sharing in the region of the vitamin D receptor (
92,
93). In addition, there has been a resurgence of interest in the theoretical aspects of mapping genes with IBD and IBS methods (
94).
APM methods have been applied to whole-genome searches only in a few cases, including a recent study on manic depression (
95). This situation is certain to change in the near future.
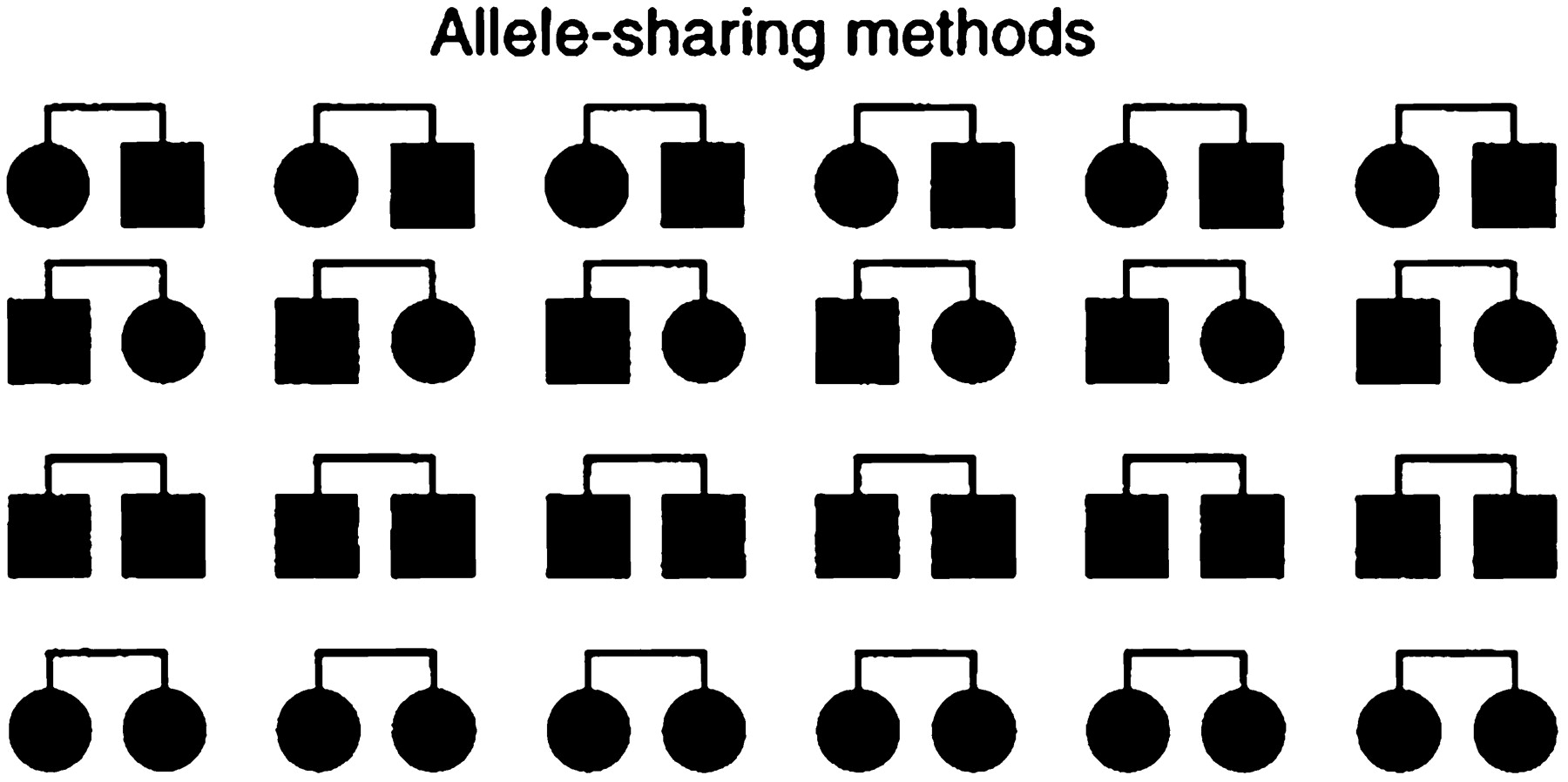
Association studies
Association studies do not concern familial inheritance patterns at all. Rather, they are case-control studies based on a comparison of unrelated affected and unaffected individuals from a population (Fig. 3). An allele A at a gene of interest is said to be associated with the trait if it occurs at a significantly higher frequency among affected compared with control individuals. The statistical analysis is simple, involving only a 2 × 2 contingency table. The biggest potential pitfall of association studies is in the choice of a control group (which is in sharp contrast to linkage and allele-sharing methods, which require no control group because they involve testing a specific model of random Mendelian segregation within a family). Although association studies can be performed for any random DNA polymorphism, they are most meaningful when applied to functionally significant variations in genes having a clear biological relation to the trait.
Association studies have played a crucial role in implicating the HLA complex in the etiology of autoimmune diseases. The allele
HLA-B27, for example, occurs in 90% of patients with ankylosing spondylitis but only 9% of the general population (
96). There are scores of HLA associations involving such diseases as type I diabetes, rheumatoid arthritis, multiple sclerosis, celiac disease, and systemic lupus erythromatosus (
97). More recently, association studies played a key role in implicating the apolipoprotein E gene in both late-onset Alzheimer’s disease and heart disease and the angiotensin converting enzyme (ACE) gene in myocardial infarction (
98). In addition, methods for assessing associations between marker loci and quantitative traits have received recent attention (
99).
What does a positive association imply about a disease? On its own, very little. Associations can arise for three reasons, one of which is completely artifactual.
1) Positive association can occur if allele A is actually a cause of the disease. In this case, the same positive association would be expected to occur in all populations (
100).
2) Positive association can also occur if allele A does not cause the trait but is in linkage disequilibrium with the actual cause, that is, A tends to occur on those chromosomes that also carry a trait-causing mutation. Linkage disequilibrium will arise in a population when two conditions are met: most cases of the trait are due to relatively few distinct ancestral mutations at a trait-causing locus, and the marker allele A was present on one of these ancestral chromosomes and lies close enough to the trait-causing locus that the correlation has not yet been eroded by recombination during the population’s history. Linkage disequilibrium is most likely to occur in a young, isolated population.
True associations due to linkage disequilibrium can yield seemingly contradictory results. Because linkage disequilibrium depends on a population’s history, a trait might show positive association with allele A
1 in one isolated population, with allele A
2 in second isolated population, and with no allele in a large, mixed population. Moreover, a trait may show no association with an Eco RI restriction fragment length polymorphism (RFLP) in a gene but strong association with a nearby Bam HI RFLP, because of the particular population genetic features of a population (
101).
3) Most disturbingly, positive association can also arise as an artifact of population admixture. In a mixed population, any trait present at a higher frequency in an ethnic group will show positive association with any allele that also happens to be more common in that group. To give a lighthearted example, suppose that a would-be geneticist set out to study the “trait” of ability to eat with chopsticks in the San Francisco population by performing an association study with the HLA complex. The allele HLA-A1 would turn out to be positively associated with ability to use chopsticks—not because immunological determinants play any role in manual dexterity, but simply because the allele HLA-A1 is more common among Asians than Caucasians.
This problem has afflicted many association studies performed in inhomogeneous populations ranging from the population of metropolitan Los Angeles to Native American tribes. A subtle example arose because Pima Amerindians are much more susceptible than Caucasians to type II diabetes. Studies in the Pima showed association between type II diabetes and the G
m locus, with the “protective” allele being the one present at higher frequency in Caucasians. Subsequent work, however, revealed that the association was apparently because tribe members have different degrees of Caucasian ancestry: The presence of a “Caucasian” allele at any gene tends to correlate with a higher degree of Caucasian ancestry, which in turn tends to correlate with a lower risk of type II diabetes (
102).
To prevent spurious associations arising from admixture, a number of steps should be taken.
1) If possible, association studies should be performed within relatively homogeneous populations. If an association can only be found in large, mixed populations but not in homogeneous groups, one should suspect admixture.
2) Given the difficulty of selecting a control group that is perfectly matched for ethnic ancestry, association studies should use an “internal control” for allele frequencies: a study of affected individuals and their parents. If the parents have genotypes A
1/A
2 and A
3/A
4 and the affected individual has geno-type A
1/A
3, then the genotype A
2/A
4 (consisting of the two alleles that the affected individual did not inherit) provides an “artificial control” that is well matched for ethnic ancestry. This method is sometimes called the affected family-based control or haplotype relative risk method and can be applied either to the genotypes or to the alleles (
103). In our opinion, such internal controls should be routinely used.
Collecting parental DNA is useful for a second, unrelated reason. With knowledge of parental genotypes, one can construct multimarker haplotypes (indicating the alleles found on the same maternally or paternally derived chromosome), which can be much more informative than studying single markers one at a time. This can be especially useful in isolated populations, where only a limited number of distinct trait-causing chromosomes may be present.
3) Once a tentative association has been found, it should be subjected to a transmission disequilibrium test (TDT) (
104,
105). The test has the premise that a parent heterozygous for an associated allele Al and a nonassociated allele A
2 should more often transmit A
1 than A
2 to an affected child. The TDT was first applied to the puzzling situation of the insulin gene, which showed strong association but no linkage to type I diabetes; linkage had been obscured because of the substantial proportion of homozygous (and thus nonsegregating) parents (
104). It should be noted that TDT cannot be directly applied to the sample in which initial association was found (because affected individuals necessarily have an excess of the associated allele) but rather to a new sample from the same population.
The controversy over a reported association between alcoholism and an allele at the dopamine D2 receptor (DRD2) illustrates all the issues in association studies. The initial study compared postmortem samples from 35 alcoholics and 35 controls, with no attempt to control for ethnic ancestry (other than race) (
106). For a Taq I RFLP located about 10 kb downstream from DRD2, the A1 allele was found to be present in 69% of alcoholics and 27% of controls. Attempts to replicate this finding, however, have yielded conflicting results, with some authors finding no association whatsoever and others reporting association for severe alcoholism only (
107). Revealingly, the frequency of the polymorphism has been shown to vary substantially among populations and among the various “control” groups used. In light of this variation, it is imperative that studies use internal control genotypes, although this has not been done to date. Association studies in relatively homogeneous populations, linkage studies, and transmission tests have all been negative (
108). At present, there is no compelling evidence that the reported association is not an artifact of admixture.
Association studies are not well suited to whole-genome searches in large, mixed populations. Because linkage disequilibrium extends over very short distances in an old population (
109), one would need tens of thousands of genetic markers to “cover” the genome. Moreover, testing many markers raises a serious problem of multiple hypothesis testing: each association test is nearly independent. Testing
n loci each with
k alleles amounts to performing about
n(
k − 1) independent tests, and the required significance level should be divided by this factor. A nominal significance level of
P ≈ 0.0001 is thus needed simply to achieve an overall false positive rate of 5%, if one tests 100 markers with six alleles each. (Some authors propose to avoid this problem by identifying all results significant at the
P = 0.05 level in an initial sample and then attempting to replicate them in a second sample (
110). However, the same multiple testing issue still applies to retesting many results at the second stage.) Genomic search for association may be more favorable in young, genetically isolated populations because linkage disequilibrium extends over greater distances, and the number of disease-causing alleles is likely to be fewer (
21,
111).
In summary, linkage-type studies and association studies have many crucial differences. Association studies test whether a disease and an allele show correlated occurrence in a population, whereas linkage studies test whether they show correlated transmission within a pedigree. Association studies focus on population frequencies, whereas linkage studies focus on concordant inheritance. One may be able to detect linkage without association (for example, when there are many independent trait-causing chromosomes in a population, so that association with any particular allele is weak) or association without linkage (for example, when an allele explains only a minor proportion of the variance for a trait, so that the allele may occur more often in affected individuals but does a poor job of predicting disease status within a pedigree). Linkage and association are often used interchangeably in popular articles about genetics, but this practice should always be avoided.
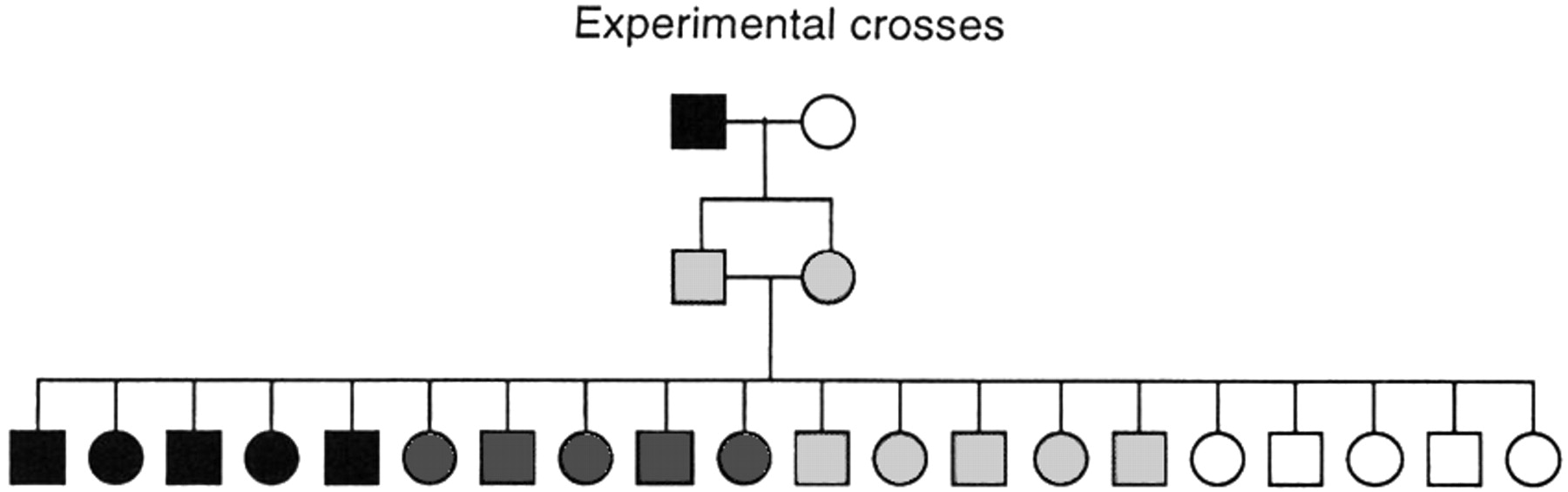
Experimental crosses: mapping polygenic traits, including QTLs
Experimental crosses of mice and rats offer an ideal setting for genetic dissection of mammalian physiology (Fig. 4). With the opportunity to study hundreds of meioses from a single set of parents, the problem of genetic heterogeneity disappears, and far more complex genetic interactions can be probed than is possible for human families. Animal studies are thus an extremely powerful tool for extending the reach of genetic analysis. Of course, animal studies must always be evaluated for their applicability to the study of human diseases. Because disease-causing mutations may occur at many steps in a pathway, animal models may not point to those genes most frequently mutated in human disease. However, animal studies should identify key genes acting in the same biochemical pathway or physiological system. Animal models that are poor models for pharmacologists seeking to evaluate a new human drug therapy may nonetheless be excellent models for geneticists seeking to elucidate the possible molecular mechanisms or pathways affected in a disease.
The power of experimental crosses is most dramatically seen in the ability to dissect quantitative traits into discrete genetic factors (
112). Systematic quantitative trait locus (QTL) mapping has only recently become possible with the construction of dense genetic linkage maps for mouse and rat (
18,
113,
114) and the development of a suitable analytical approach for a whole-genome search, known as interval mapping. Interval mapping uses phenotypic and genetic marker information to estimate the probable genotype and the most likely QTL effect at every point in the genome, by means of a maximum-likelihood linkage analysis. The basic method was introduced by Lander and Botstein for a simple situation (
47) but has been generalized to a wide variety of settings (
59,
115,
116). In general, QTL mapping is much more powerful in experimental crosses than in human families because of the fundamental differences in the statistical comparisons involved (
117) and because nongenetic noise can be decreased through the use of progeny tests, recombinant inbred strains, and recombinant congenic strains (
47,
118).
Genome-wide QTL analysis was first applied to fruit characteristics in the tomato (
119), but it was soon used in mammals to study epilepsy in mice and hypertension in rats (
113,
120). In the latter case, the animal study rapidly stimulated parallel human studies, with the reported linkage of the
ACE gene to hypertension in rats provoking investigation of various genes in the pathway and leading to the implication of angiotensinogen in essential hypertension in humans. In only a short time, there has been an explosion of interest in QTL mapping in both agriculture and biomedicine (
121). The approach opens the way to understanding the genetic basis for the tremendous strain variations seen in such quantitative traits as cancer susceptibility, drug sensitivity, resistance to infection, and aggressive behavior (
122). The most important application of QTL mapping may turn out to be the identification of modifier genes affecting single-gene traits. Yeast geneticists routinely use suppressor analysis to study a mutant gene by isolating secondary mutations capable of modifying the original mutant phenotype. Although mammalian geneticists cannot easily use mutagenesis to find suppressors, they may be able to accomplish the same goal by breeding mutations onto different genetic backgrounds and dissecting the QTLs that affect the phenotypic expression. A first such example is the finding that intestinal neoplasias induced by mutations in the mouse
Apc gene can be dramatically influenced by a modifier locus on chromosome 4 (
18). By applying this approach to the ever-growing list of gene knockouts, it should be possible to identify many additional interacting genes.
Experimental crosses also facilitate analysis of discrete traits with complex genetic etiology. Studies of type I diabetes in the nonobese diabetic mouse report the mapping of a dozen loci, each making a partial contribution to a threshold trait (
123). Analysis of type I diabetes in the BB rat points to a purely synthetic interaction with one, two, or three genes required to produce disease, depending on the particular cross (
124).
After initial mapping, experimental geneticists can study the physiological effects of individual polygenic factors by constructing congenic strains that differ only in the region of a single locus. Genes may also be mapped more finely by systematically whittling away at the size of the congenic interval. In some cases, synteny conservation in gene order between different mammals may point to interesting regions to investigate in the human genome.
An important point about the use of experimental crosses deserves to be emphasized, because it is commonly misunderstood. Genetic mapping results need not be consistent among different crosses. Linkage analysis reveals only those trait-causing genes that differ between the two parental strains used. A QTL may thus be detected in an A × B cross, but not in an A × C cross. Moreover, the effect of a QTL allele may change—or even disappear—when bred onto a different genetic background, because of epistatic effects of other genes.
Experimental design
In designing a genetic dissection, two crucial choices arise: (i) the number and type of families from which to collect data and (ii) the number and type of genetic markers to use. To make these choices, one needs to know the statistical power to detect a gene as a function of these choices.
For a simple Mendelian monogenic trait, a basic rule of thumb suffices: With a genetic map containing highly polymorphic markers every 20 centimorgans, linkage can be easily detected with about 40 informative meioses (
21,
134). More generally, the power to detect linkage depends essentially on the number of informative meioses, almost regardless of family structure. Power can be approximated simply by counting informative meioses and can be more precisely estimated with simulation-based computer packages such as SIMLINK and SLINK (
135).
In contrast, there is no comparable prescription for a complex trait. The optimal experimental design depends on the precise details of the genetic complexities, information which is typically not known in advance. The best compromise is to design a study to have sufficient power to detect any genes with effects exceeding a given magnitude. For example, one can calculate the number of sib pairs required to use allele-sharing methods to detect a locus that increases the relative risk to siblings by at least twofold (
32,
82,
136). However, even if the overall relative risk to siblings is large, there is no guarantee that there exists any individual locus having an effect of this magnitude. Similarly, one can calculate the number of progeny needed to detect a QTL accounting for 10% of the phenotypic variance of a trait, but predicting whether any such loci will be present is possible only under very favorable circumstances (
137). Genetic analyses of complex traits should always explicitly report the minimum effect that could have been reliably detected given the subjects studied.
The optimal choice of which families or crosses to study may also vary with the circumstances. For human studies, the range of choices include whether to focus on individuals with extreme phenotypes, when to extend a pedigree, and whether to prefer or to exclude families with too many affected individuals (
137). For animal studies, the issues include whether to set up a backcross or intercross and whether to concentrate on the progeny with the most extreme phenotypes (
47,
138).
The optimal density of genetic markers is a topic requiring more attention. The effect of polymorphism rate on the power of allele-sharing methods has been studied for single markers (
33,
95,
136,
139), but not for the more realistic situation of multipoint mapping. It is clear that denser maps are needed for the study of sib pairs without available parents or for the study of more distant relatives, but quantitative guidance is lacking. The effect of marker density on experimental crosses has been more extensively studied (
47,
140). Finally, a few authors have begun to explore two-tiered strategies, in which initial evidence is obtained with a sparse map and then confirmed with a dense map (
141).
Cloning genes that underlie complex traits
Once genetic dissection implicates a chromosomal region, there remains the formidable task of identifying the responsible gene. That type I diabetes cosegregates with anonymous markers on chromosome 11q in the human or that hypertension cosegregates with the ACE gene in rat crosses simply indicates that a causative gene lies somewhere nearby. However, the possible region might be as large as 10 to 20 Mb—enough to contain 500 genes. Positional cloning requires higher resolution mapping to narrow the search to a tractable region.
For a simple Mendelian trait, the situation is most favorable. Because the responsible gene must show perfect cosegregation with the trait, even a single crossover suffices to eliminate a region from consideration. From a study of 200 meioses, the interval can be pared to about 1 cM, corresponding to about 1 Mb (
142). Still, the challenge is considerable. It is sobering to note that virtually all successful positional cloning efforts have depended on the fortuitous presence of chromosomal abberrations, trinucleotide repeat expansions, or previously known candidate genes. Only two human disease genes have been positionally cloned solely on the basis of point mutations: cystic fibrosis and diastrophic dysplasia (DTD) (
143).
For complex traits, positional cloning will likely be even harder. Because cosegregation is not expected to be perfect, single crossovers no longer suffice for fine-structure mapping. Resolution becomes a statistical matter (
144). For a gene conferring a relative risk of twofold, for example, one would need to examine a median number of nearly 600 sib pairs to narrow the likely region (95% confidence interval) to 1 cM. Moreover, the genes underlying complex traits may be subtle missense mutations rather than gross deletions. How will positional cloners overcome these obstacles?
In the human, the most powerful strategy may prove to be linkage disequilibrium mapping in genetically isolated populations (
21,
145). The idea is to find many affected individuals who have inherited the same disease-causing allele from a common ancestor. Such individuals will tend to have retained the particular pattern of alleles present on the ancestral chromosome, with the immediate vicinity of the gene being evident as the region of maximal retention. In effect, the method exploits information from many historical meioses and thereby affords much higher recombinational resolution. Fine-structure linkage disequilibrium mapping has been applied to the isolated Finnish population (founded about 100 generations ago) to permit the cloning of the DTD gene (
143). Whereas conventional recombinational mapping was only able to localize the gene to within about 1.5 cM, linkage disequilibrium studies were able to pinpoint it to within about 50 kb. The approach is also applicable to younger populations: linkage disequilibrium should be detectable over larger distances, although the ultimate resolving power will be less (
146). Elegant studies in the Mennonite population (founded about 10 generations ago) have allowed initial mapping of genes involved in a recessive form of Hirschsprung disease (
20).
In animal models, fine-structure mapping of factors such as QTLs can be accomplished through appropriate breeding. The key is to ensure unambiguous genotyping at the trait-causing locus. The best solution is probably to (i) create congenic strains differing only in the region of interest, (ii) cross these strains to construct recombinant chromosomes (that is, ones in which there has been a crossover between flanking genetic markers), and (iii) evaluate each recombinant chromosome to determine which trait-causing allele is carried by performing progeny testing (that is, examining the phenotype of many progeny carrying the chromosome) (
113). The construction of the required congenic strains would traditionally require 20 generations of breeding. With the advent of complete genetic linkage maps, however, one can construct “speed congenics” in only three to four generations by using marker-directed breeding (
147).
The Human Genome Project promises to make a tremendous contribution to the positional cloning of complex traits by eventually providing a complete catalog of all genes in a relevant region. With such information, positional cloning will be reduced to the systematic evaluation of candidate genes—still challenging, but far more manageable than today’s more haphazard forays. Indeed, the Human Genome Project is essential if the genetic analysis of complex traits is to achieve its full potential.
Finally, candidate genes, whether identified by positional cloning or guessed a priori, must always be subjected to rigorous evaluation before they are accepted. The gold-standard tests for human genes should include association studies demonstrating a clear correlation between functionally relevant allelic variations and the risk of disease in humans, and transgenic studies demonstrating that gene addition or gene knockout in animals produces a phenotypic effect. For genes identified from experimental animal crosses, one can and should go a step further by demonstrating that an induced knockout allele at the candidate gene fails to complement an allele at the locus to be cloned (
148).